In this video, I'm going to introduce you to an economic model called the production possibilities frontier. So here we have a graph with the production possibilities frontier on it. We're gonna call it the PPF for short. Some books call it the PPC, but I'm gonna use PPF throughout these videos. So, the PPF is a graph showing the combinations of output an economy can produce with the available resources, right? This is what kind of mix of products can we produce with what we have, alright? So, we're gonna make some assumptions when we deal with this graph. We've got 2 goods; that's what's gonna be the production in our society. In this example, we've got the economy of Clutchtopia here creating both thin-crust pizzas and robots, right. That is what we produce in Clutchtopia: thin-crust pizza and robots. We're gonna assume we've got a fixed amount of resources, right? This involves scarcity. We don't have unlimited resources; we have a fixed amount and for our example, it's not gonna grow or shrink. We've got a certain amount of resources, a certain amount of labor, a certain amount of land, human capital, right? So, it's a certain amount of the inputs into the process. And our last assumption is that we've got fixed technology as well. Okay? So nothing's gonna be changing in this society. That's the idea. Alright. So let's go to the graph. We've got Clutchtopia, producing thin-crust pizzas and robots. So along this line is what we call the PPF. This blue line on the graph, that is Clutchtopia’s PPF. So that is the production possibilities frontier, and when we look at this graph, we're going to look at a couple of key points here. So, if we look at the point way up here on the graph where we're producing 10,000 robots up there, right? We got 10,000 robots but no pizza. So in Clutchtopia, if we put all our efforts into robot production, we could have 10,000 robots. Now let's say Clutchtopia put all their efforts into pizza production. For thin-crust pizzas, we could pop out 4,000,000 pizzas, right, but 0 robots if we were at this point down here on the graph, but we can also produce some mix of the two. Right? We can have some robots and some pizza. But we know that if we have 4,000,000 pizzas, we're not gonna be able to have any robots. Right? So 4,000,000 is the maximum amount of pizzas with no robots, but let's say we're at a point like right here. Right? We can have a mix of say 3,000,000 pizzas and 4,000 robots there, right? So anywhere along that line is still part of the mix we can attain. Right? So we've got two things to think about. We've got attainability, right? Is it attainable or unattainable, this level of production? So what we're gonna say is that anywhere inside and on the graph or, excuse me, on the PPF as well. Inside and on the line is attainable. It’s a mix of production that we can attain. Right? So what I’m saying here is yes, we could be at this line on the line here at 3,000,000 pizzas and 4,000 robots, but it’s totally possible that we could be say at this point right here in blue where we’re producing 1,000,000 pizzas and 2,000 robots. Right? That is still an attainable amount of production. Compare that to an unattainable amount. So I’m gonna write attainable here inside of yellow. Attainable. And for unattainable, I'm going to use this light blue. So anything out here, outside the graph, right, anything outside the graph is gonna be unattainable. It’s an amount of production that we cannot achieve with our current resources, our current technology. Right? So let me show you an example here. If I were to put a point out here, say, at this point in blue, now we’re saying we want 3,000,000 pizzas and 7,000 robots, and that’s just unattainable because it’s outside of the curve. So, outside of the curve is unattainable. Okay? So inside is attainable, outside is unattainable. And one more thing I wanna talk to you about real quick is productive efficiency and allocative efficiency. So we call something productively efficient if you'll scroll down a little bit, we've got here: productive efficiency is producing at any point on the PPF. So any point on the PPF is productively efficient. That means we are getting the most we can with our current situation, right? So, we're saying we're efficient if we're anywhere along the curve. So this point right here if we go back to the curve, I'm gonna start putting some points in black. All these points are productively efficient anywhere here along the graph, right. That's all productively efficient on the graph. Okay. And allocative efficiency, if you see right there below productive efficiency, that's just a little more subjective. This is that you're producing the correct mix based on consumer preferences. So that’s the idea of do the consumers of Clutchtopia, do they want 3,000,000 pizzas or do they want 1,000,000 pizzas? It all depends on the consumer choices and that's the allocative efficiency that you see, but on the graph it’s easy to tell if you’re being productively efficient. Productive efficiency is reached by being on the graph. Cool? So let’s continue and we’ll do a practice.
- 0. Basic Principles of Economics1h 5m
- Introduction to Economics3m
- People Are Rational2m
- People Respond to Incentives1m
- Scarcity and Choice2m
- Marginal Analysis9m
- Allocative Efficiency, Productive Efficiency, and Equality7m
- Positive and Normative Analysis7m
- Microeconomics vs. Macroeconomics2m
- Factors of Production5m
- Circular Flow Diagram5m
- Graphing Review10m
- Percentage and Decimal Review4m
- Fractions Review2m
- 1. Reading and Understanding Graphs59m
- 2. Introductory Economic Models1h 10m
- 3. The Market Forces of Supply and Demand2h 26m
- Competitive Markets10m
- The Demand Curve13m
- Shifts in the Demand Curve24m
- Movement Along a Demand Curve5m
- The Supply Curve9m
- Shifts in the Supply Curve22m
- Movement Along a Supply Curve3m
- Market Equilibrium8m
- Using the Supply and Demand Curves to Find Equilibrium3m
- Effects of Surplus3m
- Effects of Shortage2m
- Supply and Demand: Quantitative Analysis40m
- 4. Elasticity2h 16m
- Percentage Change and Price Elasticity of Demand10m
- Elasticity and the Midpoint Method20m
- Price Elasticity of Demand on a Graph11m
- Determinants of Price Elasticity of Demand6m
- Total Revenue Test13m
- Total Revenue Along a Linear Demand Curve14m
- Income Elasticity of Demand23m
- Cross-Price Elasticity of Demand11m
- Price Elasticity of Supply12m
- Price Elasticity of Supply on a Graph3m
- Elasticity Summary9m
- 5. Consumer and Producer Surplus; Price Ceilings and Floors3h 45m
- Consumer Surplus and Willingness to Pay38m
- Producer Surplus and Willingness to Sell26m
- Economic Surplus and Efficiency18m
- Quantitative Analysis of Consumer and Producer Surplus at Equilibrium28m
- Price Ceilings, Price Floors, and Black Markets38m
- Quantitative Analysis of Price Ceilings and Price Floors: Finding Points20m
- Quantitative Analysis of Price Ceilings and Price Floors: Finding Areas54m
- 6. Introduction to Taxes and Subsidies1h 46m
- 7. Externalities1h 12m
- 8. The Types of Goods1h 13m
- 9. International Trade1h 16m
- 10. The Costs of Production2h 35m
- 11. Perfect Competition2h 23m
- Introduction to the Four Market Models2m
- Characteristics of Perfect Competition6m
- Revenue in Perfect Competition14m
- Perfect Competition Profit on the Graph20m
- Short Run Shutdown Decision33m
- Long Run Entry and Exit Decision18m
- Individual Supply Curve in the Short Run and Long Run6m
- Market Supply Curve in the Short Run and Long Run9m
- Long Run Equilibrium12m
- Perfect Competition and Efficiency15m
- Four Market Model Summary: Perfect Competition5m
- 12. Monopoly2h 13m
- Characteristics of Monopoly21m
- Monopoly Revenue12m
- Monopoly Profit on the Graph16m
- Monopoly Efficiency and Deadweight Loss20m
- Price Discrimination22m
- Antitrust Laws and Government Regulation of Monopolies11m
- Mergers and the Herfindahl-Hirschman Index (HHI)17m
- Four Firm Concentration Ratio6m
- Four Market Model Summary: Monopoly4m
- 13. Monopolistic Competition1h 9m
- 14. Oligopoly1h 26m
- 15. Markets for the Factors of Production1h 33m
- The Production Function and Marginal Revenue Product16m
- Demand for Labor in Perfect Competition7m
- Shifts in Labor Demand13m
- Supply of Labor in Perfect Competition7m
- Shifts in Labor Supply5m
- Differences in Wages6m
- Discrimination6m
- Other Factors of Production: Land and Capital5m
- Unions6m
- Monopsony11m
- Bilateral Monopoly5m
- 16. Income Inequality and Poverty35m
- 17. Asymmetric Information, Voting, and Public Choice39m
- 18. Consumer Choice and Behavioral Economics1h 16m
Production Possibilities Frontier (PPF) - Introduction and Productive Efficiency: Study with Video Lessons, Practice Problems & Examples
 Created using AI
Created using AIThe production possibilities frontier (PPF) illustrates the maximum output combinations of two goods, such as thin crust pizzas and robots, given fixed resources and technology. Points on the PPF represent productive efficiency, while those inside indicate attainable production levels. Points outside the curve are unattainable. Allocative efficiency depends on consumer preferences for the mix of goods produced. Understanding opportunity cost and the trade-offs involved in production decisions is crucial for economic analysis and resource allocation.
The PPF helps us understand scarcity and opportunity costs. Wow!
Understanding the PPF
Video transcript
PPF - Attainable and Efficient
Video transcript
Alright. So let's go ahead and do this example, that uses the graph at the top of this page. Assume Clutchetopia features the curve illustrated above. Mark the following levels of production as attainable or unattainable. If production is attainable, mark the level of production as efficient or inefficient. Okay. So we've got different levels of production here, and let's go ahead and just start with the first one here. We're saying that Clutchetopia should produce 5,000,000 pizzas and 3,000 robots. Okay. 5,000,000 pizzas and 3,000 robots. Let's go up to our graph, and let's find that point on the graph. So we're going to go to 5,000,000 pizzas here and 3,000 robots, and if we find that point, that puts us right here right? And this is outside of the graph, right? Outside of the so this point is unattainable, right? Based on our previous discussion, if it's outside of the graph, it is unattainable. So our discussion about efficiency doesn't matter because it's unattainable, so there's no way it could be efficient or inefficient, because we can't even attain it. So we're just going to put an NA here.
Okay. Let's try the next one. 1,000,000 pizzas and 9,000 robots. So back on our graph, let's find that point. 1,000,000 pizzas 9,000 robots. So here's 1,000,000 pizzas. If we go up from 1,000,000 and we go to 9 on the robots, and we're going to find that point. And that point lies right there at 9,000 robots and 1,000,000 pizzas. We know that if it's on or inside the graph, it is attainable, and then if it's on the curve, we know that it's productively efficient. So in this case, we have both an attainable and efficient amount because we're on the curve. So we have attainable and efficient. We are getting the most that we can with our resources at that production mix. So it's productively efficient.
Let's try the next one. 4,000,000 pizzas and 0 robots. So let's go to our graph and let's find that point. So we've got 4,000,000 pizzas and 0 robots, this point is already on here in green, let me highlight it in red here. So 4,000,000 pizzas and 0 robots. We're right here down on the x-axis. So what do you think? Is this point attainable or unattainable? Well, it looks kind of weird because it's on the axis. We're not producing any robots, but we are still on the curve. So we've got 4,000,000 pizzas and 0 robots. That is an attainable amount, and it's efficient because it is on the curve. So we've got an attainable efficient amount here.
Let's try the next one, 3,000,000 pizzas and 3,000 robots. So now we've got 3,000,000 pizzas and 3,000 robots. We are going to go up from 3,000,000 pizzas, over from 3,000 robots, and end up at this red point right here. Notice we're not on the curve. We're just inside of it. We didn't reach that perfect production efficiency. We are just inside. So, yes, we can attain this level of production, but it's not efficient because we could be producing a little bit more robots or a little bit more pizza with our current resources and technology. So we have an attainable amount, but it is inefficient. So we're going to put an I there for inefficient.
Alright, let's try the last one. 2,000,000 pizzas and 7,000 robots. So here we go, 2,000,000 pizzas right here and let's find 7,000. 7 will be right up here. So this red dot that I'm adding now is going to be 2,000,000 and 7,000 notice that lies right on our curve so again we've reached productive efficiency. Oh, had a weird scroll there. Give me one second to get back to where we were, and oh boy. There we go. We've got an attainable efficient amount. Alright? So that last one is attainable and efficient. Cool, guys. Hope you got that. Let's move on to the next video.
A point inside the production possibilities frontier is
The economy of Clutchtopia can be summarized as seen on the PPF below. Consider the production mixes denoted alongside the graph. Mark the levels of production as Attainable (A) or Unattainable (U). If production is attainable, mark the level of production as Efficient (E) or Inefficient (I).
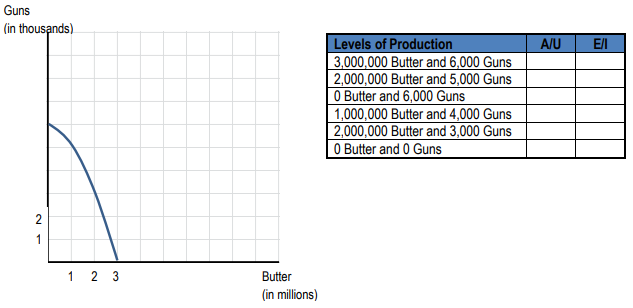
Problem Transcript
Here’s what students ask on this topic:
What is the Production Possibilities Frontier (PPF) and what does it illustrate?
The Production Possibilities Frontier (PPF) is a graph that shows the maximum possible output combinations of two goods that an economy can produce given fixed resources and technology. It illustrates the trade-offs and opportunity costs involved in production decisions. Points on the PPF represent productive efficiency, meaning the economy is utilizing all its resources efficiently. Points inside the PPF are attainable but indicate underutilization of resources, while points outside the PPF are unattainable with the current resources and technology.
 Created using AI
Created using AIWhat is the difference between productive efficiency and allocative efficiency?
Productive efficiency occurs when an economy is producing at any point on the PPF, meaning it is using all its resources efficiently without any waste. Allocative efficiency, on the other hand, is more subjective and depends on consumer preferences. It occurs when the mix of goods being produced represents the combination that consumers most desire. While productive efficiency is about maximizing output, allocative efficiency is about producing the right mix of goods to satisfy consumer preferences.
 Created using AI
Created using AIWhat does a point inside the PPF indicate?
A point inside the PPF indicates that the economy is not utilizing all its resources efficiently. This means that it is possible to increase the production of one or both goods without sacrificing the production of the other. Points inside the PPF represent attainable production levels but indicate underutilization of resources, such as labor, capital, or technology.
 Created using AI
Created using AIWhat does a point outside the PPF represent?
A point outside the PPF represents an unattainable level of production with the current resources and technology. It indicates a combination of goods that the economy cannot produce given its existing constraints. To reach such a point, the economy would need to increase its resources, improve technology, or find more efficient ways to produce goods.
 Created using AI
Created using AIHow does opportunity cost relate to the PPF?
Opportunity cost is a key concept illustrated by the PPF. It represents the cost of forgoing the next best alternative when making a production decision. On the PPF, moving from one point to another involves shifting resources from the production of one good to another, which incurs an opportunity cost. For example, producing more robots in Clutchtopia means producing fewer thin crust pizzas, and the opportunity cost is the number of pizzas forgone to produce additional robots.
 Created using AI
Created using AI