Atomic masses of elements can be found by simply looking at the periodic table. So let's start off by looking at the symbol of H, which represents hydrogen. And if you take a look at hydrogen as well as the other elements on the periodic table, you'll see these whole numbers. These whole numbers represent our atomic number. They are the number of protons. When we say atomic mass though, the atomic mass is the number that is seldom a whole number. This is our atomic mass. So you can find the atomic mass of any element on the periodic table just by simply looking it up. Now we're going to say the atomic mass itself is an average of all its isotopes that use the units of grams per mole, AMU, or Daltons, and we're going to say remember that 1AMU = 1.66×10-27kg. So just remember, these atomic masses that you see on the periodic table, they are usually not whole numbers. You'd have to get way down below here to these heavy elements down here till you see whole numbers for atomic masses. And remember, they are the average of all the isotopes for that given element.
- 1. The Chemical World9m
- 2. Measurement and Problem Solving2h 25m
- 3. Matter and Energy2h 15m
- Classification of Matter18m
- States of Matter8m
- Physical & Chemical Changes19m
- Chemical Properties8m
- Physical Properties5m
- Temperature (Simplified)9m
- Law of Conservation of Mass5m
- Nature of Energy5m
- First Law of Thermodynamics7m
- Endothermic & Exothermic Reactions7m
- Heat Capacity16m
- Thermal Equilibrium (Simplified)8m
- Intensive vs. Extensive Properties13m
- 4. Atoms and Elements2h 33m
- The Atom (Simplified)9m
- Subatomic Particles (Simplified)12m
- Isotopes17m
- Ions (Simplified)22m
- Atomic Mass (Simplified)17m
- Periodic Table: Element Symbols6m
- Periodic Table: Classifications11m
- Periodic Table: Group Names8m
- Periodic Table: Representative Elements & Transition Metals7m
- Periodic Table: Phases (Simplified)8m
- Periodic Table: Main Group Element Charges12m
- Atomic Theory9m
- Rutherford Gold Foil Experiment9m
- 5. Molecules and Compounds1h 50m
- Law of Definite Proportions9m
- Periodic Table: Elemental Forms (Simplified)6m
- Naming Monoatomic Cations6m
- Naming Monoatomic Anions5m
- Polyatomic Ions25m
- Naming Ionic Compounds11m
- Writing Formula Units of Ionic Compounds7m
- Naming Acids18m
- Naming Binary Molecular Compounds6m
- Molecular Models4m
- Calculating Molar Mass9m
- 6. Chemical Composition1h 23m
- 7. Chemical Reactions1h 43m
- 8. Quantities in Chemical Reactions1h 16m
- 9. Electrons in Atoms and the Periodic Table2h 32m
- Wavelength and Frequency (Simplified)5m
- Electromagnetic Spectrum (Simplified)11m
- Bohr Model (Simplified)9m
- Emission Spectrum (Simplified)3m
- Electronic Structure4m
- Electronic Structure: Shells5m
- Electronic Structure: Subshells4m
- Electronic Structure: Orbitals11m
- Electronic Structure: Electron Spin3m
- Electronic Structure: Number of Electrons4m
- The Electron Configuration (Simplified)20m
- The Electron Configuration: Condensed4m
- Ions and the Octet Rule9m
- Valence Electrons of Elements (Simplified)5m
- Periodic Trend: Metallic Character4m
- Periodic Trend: Atomic Radius (Simplified)7m
- Periodic Trend: Ionization Energy (Simplified)9m
- Periodic Trend: Electron Affinity (Simplified)7m
- Electron Arrangements5m
- The Electron Configuration: Exceptions (Simplified)12m
- 10. Chemical Bonding2h 10m
- Lewis Dot Symbols (Simplified)7m
- Ionic Bonding6m
- Covalent Bonds6m
- Lewis Dot Structures: Neutral Compounds (Simplified)8m
- Bonding Preferences6m
- Multiple Bonds4m
- Lewis Dot Structures: Multiple Bonds10m
- Lewis Dot Structures: Ions (Simplified)8m
- Lewis Dot Structures: Exceptions (Simplified)12m
- Resonance Structures (Simplified)5m
- Valence Shell Electron Pair Repulsion Theory (Simplified)4m
- Electron Geometry (Simplified)7m
- Molecular Geometry (Simplified)9m
- Bond Angles (Simplified)11m
- Dipole Moment (Simplified)14m
- Molecular Polarity (Simplified)7m
- 11 Gases2h 15m
- 12. Liquids, Solids, and Intermolecular Forces1h 11m
- 13. Solutions3h 1m
- 14. Acids and Bases2h 14m
- 15. Chemical Equilibrium1h 27m
- 16. Oxidation and Reduction1h 33m
- 17. Radioactivity and Nuclear Chemistry53m
Atomic Mass (Simplified): Study with Video Lessons, Practice Problems & Examples
 Created using AI
Created using AIAtomic masses of elements, found on the periodic table, represent averages of all isotopes and are typically not whole numbers. The atomic mass can be calculated using isotopic masses and their percent abundances, which can be converted to fractional abundance. The formula for atomic mass is: . Understanding these concepts is crucial for grasping atomic theory and chemical properties.
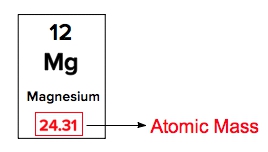
The atomic mass of an element can be found on the Periodic Table.
Determining Atomic Mass
Atomic Mass (Conceptual) Concept 1
Video transcript
Atomic Mass (Conceptual) Example 1
Video transcript
So here for this example question, it says, which of the following represents an element from the first column with the greatest atomic mass? Alright. So our first column, if we look at this periodic table, our first column is this with all of these different elements. And remember, the number in red, which is not a whole number normally, that represents the atomic mass of any of these given elements. Now here, if we take a look, we have barium, Ba. Again, later we'll learn about how the names are attached to the element symbol. Ba is not in the 1st column; here it's in the 2nd column. So this cannot be a choice. Then we're going to say next that we have Al. Al stands for aluminum. Aluminum is over here in the 3rd column, well, all the way over here in this 13th column, actually, so this is out. Next, we have Cs, this is cesium. Here it is right here. It's in the first column. It's pretty low down there. Its atomic mass is 132.91, which could be in grams per mole, atomic mass units, or Daltons. So far, it looks like it's the highest one. The only one higher than that would be Fr. Notice that in the bottom rows here, most of them are whole numbers. These are super-large mass elements that are pretty unstable. They typically don't have numerous isotopes. As a result, they have no decimal places. So, so far, C looks like it's our best choice. If we look at D, we have Li, which is up here, not higher in mass, not greater in atomic mass. And then we have Na, which is right here. So it looks like C is our best choice. It has the greatest mass, atomic mass, from column 1 from the choices provided. So just remember we have our element symbols, we have our atomic masses, which normally are not whole numbers, and then we actually have whole numbers. Those represent our atomic numbers.
On the Periodic Table, the atomic mass is represented by the number with decimal places.
Which of the following choices has the greatest atomic mass?
Atomic Mass (Simplified) Concept 2
Video transcript
Now the atomic mass of an element can be calculated if you know the isotopic masses and percent abundances. Isotopic masses are the masses for all the isotopes of a given element. Percent abundance, sometimes referred to as natural abundances, are the percentages available for each of the isotopes of a given element. Sometimes they're also referred to as percent natural abundances. I know it's a little redundant, but just remember, you might see percent abundances, natural abundances, or percent natural abundances.
Isotopic abundance, also called your fractional abundance, is your percent abundance of an isotope divided by 100. When you divide a percentage by 100, you're changing it from its percentage form to its fractional or decimal form.
All of this together gives us our atomic mass formula. The atomic mass formula is: atomicmass= m1f1 + m2f2 + ... + mifi where mi is the isotopic mass of isotope i, and fi is its fractional abundance. Of course, if you have more than 2 isotopes for a given element, you would keep adding, for example, plus the isotopic mass of isotope 3 times its isotopic abundance plus isotope mass 4 times its isotopic abundance. In this example, we're just showing that this particular element we're talking about has 2 isotopes involved with it, and they both have their own masses. However, this formula can be expanded to include more isotopes, depending on the element. Elements such as manganese have various isotopes, so their formulas would be larger.
Atomic Mass (Simplified) Example 2
Video transcript
In the following example question, it says, calculate the atomic mass of gallium if gallium has 2 naturally occurring isotopes with the following masses and natural abundances. So here we're dealing with gallium 69 and 71. Their atomic masses are written in terms of atomic mass units, and then here we have 60.11% and 39.89%. Those represent the percent abundances. Now, to find the atomic mass of our gallium element, let's follow step 1. Step 1 says, if you are given percent abundances, which we were, we're going to divide them by 100 in order to isolate our fractional abundances. So, divide them both by 100; when we do that, we're going to get our fractional abundances. Step 2, plug your given variables into the atomic mass formula in order to isolate the missing variable. So this is just a simple plug and chug algebraic type of situation. Our atomic mass of our element equals the mass of the first isotope times its fractional abundance plus the mass of our second isotope times its fractional abundance. So, when we do that, we're going to get 69.72304099AMU. Since our isotopic masses have 4 decimal places, we could follow 4 decimal places here, but we have multiple choice options, and we're going to go with the best answer, which would be option a for this particular question. So, using the atomic mass formula is pretty simple. All we have to do is round up all the variables that you're given and isolate the one that's missing. From there, you can find your final answer.
Only three isotopes of magnesium exist on earth. 24Mg is the most common form at 78.70% natural abundance with a mass of 23.98504 amu, 25Mg has a 10.13% natural abundance, while 26Mg has a natural abundance of 11.17% and a mass of 25.98259 amu. What is the mass of the 25Mg isotope?
Silver has an atomic mass of 107.868 amu. The Ag-109 isotope (108.905 amu) is 48.16%. What is the amu of the other isotope?
Here’s what students ask on this topic:
What is atomic mass and how is it different from atomic number?
Atomic mass is the weighted average mass of an element's isotopes, measured in atomic mass units (AMU) or Daltons. It is seldom a whole number because it accounts for the different isotopes and their abundances. Atomic number, on the other hand, is the number of protons in an atom's nucleus and is always a whole number. The atomic number defines the element, while the atomic mass provides information about the isotopic composition of the element.
 Created using AI
Created using AIHow do you calculate the atomic mass of an element?
To calculate the atomic mass of an element, you need the isotopic masses and their percent abundances. The formula is:
Convert percent abundances to fractional abundances by dividing by 100. Multiply each isotopic mass by its fractional abundance and sum the results to get the atomic mass.
 Created using AI
Created using AIWhy are atomic masses on the periodic table not whole numbers?
Atomic masses on the periodic table are not whole numbers because they represent the weighted average of all the isotopes of an element, taking into account their relative abundances. Since isotopes have different masses and occur in different proportions, the average is usually a decimal value. This average reflects the natural isotopic distribution of the element.
 Created using AI
Created using AIWhat is the significance of isotopic abundance in calculating atomic mass?
Isotopic abundance, also known as percent abundance, indicates the relative proportion of each isotope of an element in a natural sample. It is crucial for calculating atomic mass because the atomic mass is a weighted average of the isotopic masses, based on their abundances. Without knowing the isotopic abundances, you cannot accurately determine the atomic mass of an element.
 Created using AI
Created using AIWhat units are used to express atomic mass?
Atomic mass is typically expressed in atomic mass units (AMU) or Daltons (Da). One atomic mass unit is defined as one-twelfth the mass of a carbon-12 atom, which is approximately 1.66 × 10-27 kilograms. These units are used because they are convenient for expressing the very small masses of atoms and molecules.
 Created using AI
Created using AI