Density of Geometric Objects: Study with Video Lessons, Practice Problems & Examples

Density is defined as mass per volume, and it can be applied to geometric objects like spheres, cubes, and cylinders. The volume of a sphere is given by 43π×r3, where r is the radius. For a cube, the volume is a3, with a as the edge length. A cylinder's volume is calculated using V=πr2×h, incorporating both radius and height.

Density of Geometric Objects Concept

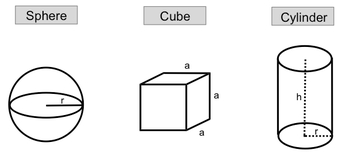
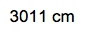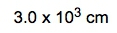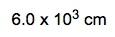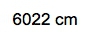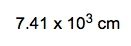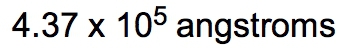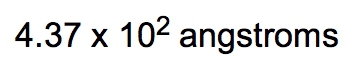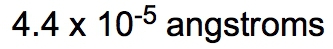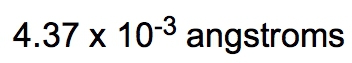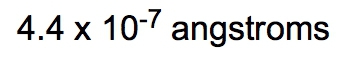So we understand that density is just mass per volume. Now we're going to take that idea of density and apply it to geometric objects. We're going to say here, when given the mass of a geometric object, you can relate it to its volume and density. Our typical geometric objects are a sphere, a cube, and a cylinder. Each one of them has their own volume equation, which can later on relate to density if we wish. So here we have a sphere. Now in this sphere, we have our radius. Remember, the radius is just the distance from the center to the edge of the sphere. When it comes to a sphere, its volume equation is V=43⋅π⋅r3. Notice none of these formulas we're going to write are in purple boxes, which means you don't need to commit it to memory. Typically, when it comes to volumes of geometric objects, your professor will give it to you within the question or on a formula sheet. Now when it comes to a cube, a cube has all these sides, which we label a. In a cube, we assume that they're all of equal length. As a result of this, the volume of a cube is equal to a3, where again a is equal to the length or the edge of that cube. Finally, we have a cylinder, and in the cylinder, we have to take into account 2 variables. We have the height of the cylinder, and we have, of course, again the radius of the cylinder. Taking these 2 into perspective, when it comes to a cylinder, we have volume equals V=π⋅r2⋅h. So now we're going to take a look at density questions, which relate to these different types of geometric objects.

Density of Geometric Objects Example

So, here in this example question, it says, the density of silver is 10.5 grams per centimeter³. What is the mass in kilograms of a cube of silver that measures 0.56 meters on each side? All right. Although we're talking about density here and we're talking about a cube, we can still apply the rules that we learn when it comes to given amounts, conversion factors, and end amounts. So, in this question, our given amount is the one that has only one unit connected to it, and that would be our 0.56 meters. So this is our given amount. Then we have to think about where is our end amount. Where do we need to go, and where do we stop? Our end amount here would be kilograms. So, we need kilograms from the silver cube. Next, we look to see what kind of conversion factors are available. Here we have the density of the silver. Remember, density itself is a conversion factor because it's tying together two different units, so that would be 10.5 grams per 1 centimeter³. All right. So now let's put it all together.

Given here we have the given amount, we have to get to the end amount. And remember to connect them together, we use our conversion factors. Now, we see our conversion factor here is 10.5 grams per centimeter³. We can try to isolate these grams here. If I can isolate those grams, I can convert them later into kilograms. But to be able to isolate those grams, I have to cancel out the centimeters³. Remember, centimeters³ is just a unit for volume. Sometimes we're given an amount, we have our given amount, but sometimes we have to change it up. We have to change it so that we can use it within our dimensional analysis setup. Since this whole section is on the density of geometric objects and we have a cube, I can determine the volume of the cube. Remember, volume equals length cubed. So that’d be 0.56 meters cubed. So that comes out to be 0.175616 meters³, which equals 175616 cm³

.

This is my actual given amount that I'm going to utilize within this setup, and I need to change it to meters³ because from there, I can convert it to centimeters³, and then from centimeters³, I'll be able to cancel out the centimeters from the density and be left with grams. All right. So our conversion factor 1 is just a metric prefix conversion. Meters go here on the bottom, centimeters go here on top. Remember, the coefficient of 1 goes on the same side with the metric prefix, so 1 centi is 10 to the negative 2. Here, these meters are cubed, but these are not, so I would have to cube the whole thing. Then we're going to have our meters cubed cancel out, and now we have centimeters cubed. Because it's in centimeters cubed, I can now use my conversion factor 2. So my conversion factor 2, I bring this down, 10.5 grams, 1 centimeter³ on the bottom, centimeters cubes will cancel out, and now I have grams of my substance. But I don't want it in grams. I need it in kilograms. So one more conversion factor is actually another metric prefix conversion. So we're going to put here grams on the bottom, kilograms on top. Remember, kilo is a metric prefix, so 1 kilo is 10 to the 3. So grams here cancel out, and I'll be left with kilograms at the end. So when you plug this in initially, it'll be ( 0.175616 10^-2 ) × 10.5 ÷ 103 , if you plug this in correctly, you'll get 1,843.968 kilograms. But looking back on the original question, 0.56 has two significant figures, and 10.5 has three significant figures. So, we have to go with the least number of significant figures. So, converting this to two significant figures, we can write it either as 1800 kilograms or 1.8 × 103 kilograms . Either one is a reliable or reasonable answer. So just remember, sometimes our dimensional analysis setup, the given amount, has to be changed a little bit in order to fit and cancel out with other present units. By doing that, we're able to isolate our kilograms within this example.

Now that we've done this question, let's move on to our practice question.

A copper wire (density = 8.96 g/cm³) has a diameter of 0.32 mm. If a sample of this copper wire has a mass of 21.7 g, how long is the wire?

• A.
• B.
• C.
• D.
• E.

If the density of a certain spherical atomic nucleus is 1.0 x 10¹⁴ g/cm³ and its mass is 3.5 x 10^-23 g, what is the radius in angstroms? (Å= 10⁻¹⁰ m)

• A.
• B.
• C.
• D.
• E.

Here’s what students ask on this topic:

What is the formula for the volume of a sphere and how is it derived?

The volume of a sphere is given by the formula:

$\frac{4}{3}\pi r^3$

where $r$ is the radius of the sphere. This formula is derived using integral calculus, specifically by integrating the surface area of infinitesimally thin spherical shells from the center to the surface of the sphere.

How do you calculate the density of a cube if you know its mass and edge length?

To calculate the density of a cube, you need to know its mass ($m$) and the length of its edge ($a$). The volume of the cube is given by:

$a^3$

Density ($\rho$) is mass per unit volume, so:

$\frac{m}{a^3}$

What is the volume formula for a cylinder and what variables does it include?

The volume of a cylinder is calculated using the formula:

$\pi r^{2}h$

where $r$ is the radius of the base of the cylinder and $h$ is the height of the cylinder. This formula accounts for the area of the circular base ($\pi r^2$) multiplied by the height.

How can you find the density of a sphere if you know its mass and radius?

To find the density of a sphere, you need its mass ($m$) and radius ($r$). The volume of the sphere is given by:

$\frac{4}{3}\pi r^3$

Density ($\rho$) is mass per unit volume, so:

$\frac{m}{\frac{4}{3}\pi r^3}$

What are the typical geometric objects used to study density and their volume formulas?

The typical geometric objects used to study density are spheres, cubes, and cylinders. Their volume formulas are:

1. Sphere: $\frac{4}{3}\pi r^3$

2. Cube: $a^3$

3. Cylinder: $\pi r^{2}h$

where $r$ is the radius, $a$ is the edge length, and $h$ is the height.