Enantiomers vs Diastereomers: Study with Video Lessons, Practice Problems & Examples

Stereoisomers have the same molecular formula and connectivity but differ in spatial orientation. Enantiomers are chiral molecules that are non-superimposable mirror images, with opposite configurations at all chiral centers. In contrast, diastereomers are stereoisomers that are not mirror images, sharing some chiral centers while differing in others. The number of stereoisomers can be calculated using the formula $2^n$, where n is the number of chiral centers, indicating the complexity of stereochemistry in organic compounds.

Enantiomers vs Diastereomers Concept 1

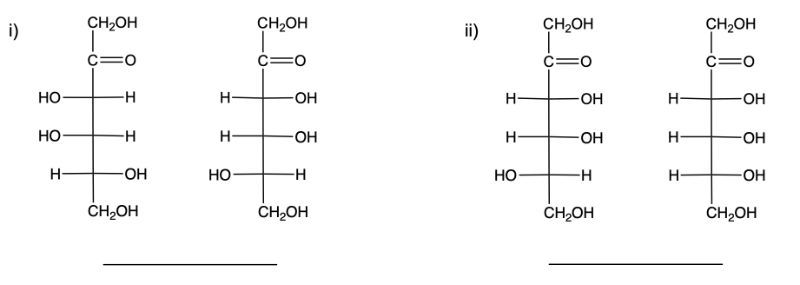
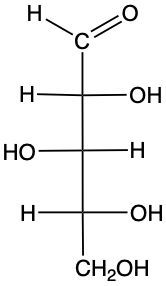
In this video, we're going to take a look at enantiomers versus diastereomers. Now, first recall that stereoisomers have the same molecular formula and connectivity, but different spatial orientation. When we talk about enantiomers, enantiomers themselves are chiral molecules with non-superimposable mirror images of each other. Basically, this means when you're comparing two chiral molecules to one another, when they have opposite configurations of each other at all their chiral centers, they are enantiomers of each other. Diastereomers. Diastereomers are stereoisomers that are not mirror images of each other. So, how do you tell if two things are diastereomers of each other? Well, when you're comparing the two to each other, some of the chiral centers will be the same in both structures, and some of them will be different. That's how we're able to tell the difference between diastereomers and enantiomers. Enantiomers, all the chiral centers are different from each other. Diastereomers, some of the chiral centers change, and some of them are the same. So, if we take a look here, we have two chiral centers here and here. And if we look right next to it, we have this structure which has two chiral centers as well. The OHs are on the opposite side. If you were to imagine a mirror was here, and this was to look into the mirror, it would see this structure here as its reflection. So, they are mirror images of each other; they are enantiomers. Then, if we compare, let's say that this is structure a, we'll say this is b, let's say this is c, and then let's say this one over here is d. If we compared a to c, what do we recognize? We recognize here that this chiral center, the OH is on the right. This chiral center, the OH is still on the right. They're the same. But if we look at the second chiral center, the OHs are on different sides. So, one chiral center stayed the same, and one changed. They would be diastereomers of each other. Then if we looked at c and d, imagine there's a mirror here, this looks into the mirror, it would see D as its reflection. So these two are enantiomers of each other. Again, enantiomers are mirror images of each other, meaning their chiral centers are opposite at all chiral centers from each other. Diastereomers are non-mirror images; they're still stereoisomers. That just means that if you're comparing two structures, in both structures, some of the chiral centers will be the same, some will be different. Now, connected to this is the number of stereoisomers, and that's the formula 2n, where n equals our number of chiral centers. So, if we take a look here, let's say we're looking at structure A, and they only gave me structure A, and they asked how many possible stereoisomers exist from structure A? It has two chiral centers, so it'd be 22, which would mean that we have a possibility of four stereoisomers, which is what we see. We see A, B, C, and D, four different stereoisomers from the fact that structure A had two chiral centers to begin with. Alright. So, just keep this in mind when we're talking about enantiomers versus diastereomers and trying to determine the total number of stereoisomers.

Enantiomers vs Diastereomers Example 1

Circle all chiral centers in the following monosaccharide and state the number of possible stereoisomers. So remember, a chiral center is where we have a carbon connected to four different groups. If we're to take a look here, our chiral centers would be three chiral centers. And we know that those are the chiral centers because those are carbons connected to four different groups. This carbon here is not a chiral center because it is forming a double bond, so it can't make four individual single bonds. This Carbon here is connected to two Hydrogens, so it can't have four different groups. And same with this one. So again, we have three chiral centers here, and the number of possible stereoisomers is based on the formula 2n, where n is the number of chiral centers. So this will be 23, which is 2 times 2 times 2, which means we have a total of 8 possible stereoisomers from this original monosaccharide. So those will be our two answers. Three chiral centers with a possibility of 8 total stereoisomers.

Identify each pair of carbohydrates as enantiomers or diastereomers.

• A. diastereomer, enantiomer 
• B. enantiomer, diastereomer 
• C. enantiomer, enantiomer 
• D. diastereomer, diastereomer

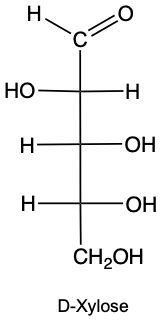
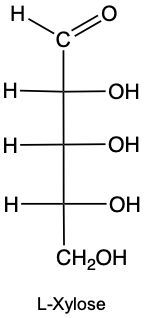
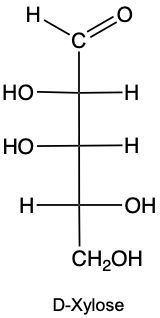
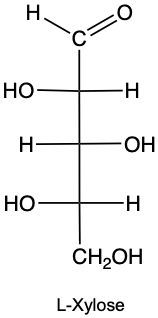
Draw the enantiomer of given structure of Xylose, and identify as D or L.

• A.
• B.
• C.
• D.

Here’s what students ask on this topic:

What is the difference between enantiomers and diastereomers?

Enantiomers are chiral molecules that are non-superimposable mirror images of each other, meaning they have opposite configurations at all chiral centers. In contrast, diastereomers are stereoisomers that are not mirror images of each other. They share some chiral centers while differing in others. This distinction is crucial in stereochemistry, as enantiomers have identical physical properties except for their interaction with plane-polarized light and reactions in chiral environments, whereas diastereomers can have different physical and chemical properties.

How can you determine if two molecules are enantiomers?

To determine if two molecules are enantiomers, you need to check if they are non-superimposable mirror images of each other. This means that they must have opposite configurations at all chiral centers. If you can place a mirror between the two molecules and they appear as mirror images, then they are enantiomers. Additionally, enantiomers will have identical physical properties except for their optical activity, where they will rotate plane-polarized light in opposite directions.

How do you identify diastereomers among stereoisomers?

Diastereomers are identified by comparing the configurations at each chiral center. Unlike enantiomers, diastereomers are not mirror images of each other. Some chiral centers will have the same configuration, while others will differ. For example, if two molecules have two chiral centers, and one chiral center is the same while the other is different, they are diastereomers. This partial similarity and difference in chiral centers distinguish diastereomers from enantiomers.

What is the formula to calculate the number of stereoisomers for a molecule?

The number of stereoisomers for a molecule can be calculated using the formula $2^n$, where $n$ is the number of chiral centers in the molecule. For example, if a molecule has 2 chiral centers, the number of possible stereoisomers is $2^2$ = 4. This formula helps in understanding the complexity and diversity of stereoisomers in organic compounds.

Why are enantiomers important in pharmaceuticals?

Enantiomers are crucial in pharmaceuticals because they can have different biological activities. One enantiomer of a drug may be therapeutically beneficial, while the other could be inactive or even harmful. This is due to the chiral nature of biological systems, which can interact differently with each enantiomer. Therefore, understanding and controlling the enantiomeric composition of drugs is essential for their safety and efficacy.