Here are the essential concepts you must grasp in order to answer the question correctly.
Crystal Structure
Crystal structure refers to the orderly arrangement of atoms in a crystalline material. In metals, atoms are typically arranged in specific geometric patterns, which can be classified into different types of unit cells, such as face-centered cubic (FCC), body-centered cubic (BCC), or hexagonal close-packed (HCP). Understanding the crystal structure is essential for determining the properties of the metal, including its density and atomic packing.
Recommended video:
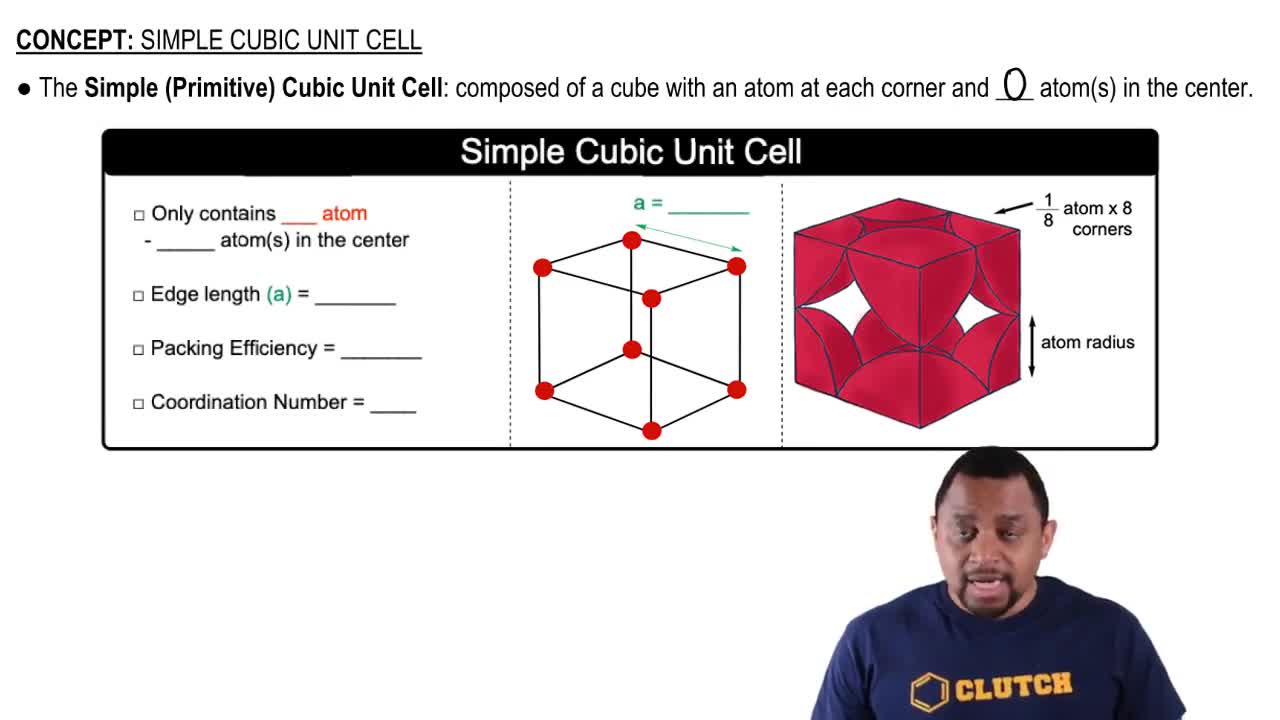
Unit Cell
A unit cell is the smallest repeating unit in a crystal lattice that reflects the symmetry and structure of the entire crystal. It is defined by its dimensions and the arrangement of atoms within it. The type of unit cell influences the density and other physical properties of the material. Identifying the correct unit cell type is crucial for understanding how titanium crystallizes.
Recommended video:
Density and Atomic Radius Relationship
The density of a material is related to its atomic mass and the volume occupied by its atoms in the crystal lattice. The atomic radius helps determine the volume of the unit cell, which is essential for calculating density. For metals like titanium, knowing the atomic radius allows us to infer the type of unit cell and how closely packed the atoms are, which is vital for answering questions about crystallization.
Recommended video:
Atomic Radius and Density of Transition Metals Example
 Verified step by step guidance
Verified step by step guidance