Introduction to Matrices: Study with Video Lessons, Practice Problems & Examples

Understanding matrices is essential for organizing information in a grid format, specifically in systems of equations. An augmented matrix represents coefficients and constants, facilitating operations like row swapping, multiplying, and adding to achieve row echelon form. This form features ones along the diagonal and zeros below, allowing for straightforward back substitution to solve for variables. Transitioning to reduced row echelon form further simplifies the process, yielding direct solutions without additional steps. Mastery of these concepts enhances problem-solving skills in algebra, particularly with multivariable polynomials and their coefficients.

Introduction to Matrices

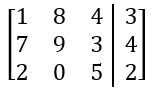
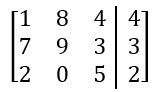
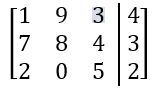
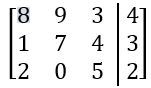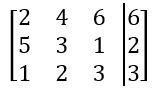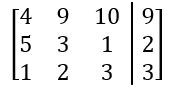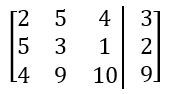Everyone. Welcome back. So we've spent a lot of time talking about systems of equations in the last few videos. We're going to shift gears a little bit. We're going to start talking about a new idea called a matrix, or the plural version is matrices. Now matrices can seem kind of scary at first because you'll see these big blobs of brackets with numbers inside them and all that stuff. But I'm actually going to break it down for you, and I'm going to show you that a matrix is really just a way to organize information or numbers into a grid-like pattern with rows and columns. Alright? So let's go ahead and get to it. I'm going to break it down for you. Alright? So we've got this matrix here, and the way we sort of define a matrix or we label these sort of parts of a matrix is by rows and columns. There are 2 rows in this matrix. We have 1 and 2. Those go horizontally, and we also have 3 columns in this matrix. Right? So 3 columns. So this is just 1 2 3. Alright? Now, so you might see this matrix referred to as a 2 by 3 matrix, 2 rows, 3 columns. Alright? Now, really, all this matrix is just a way to sort of arrange numbers, and you'll actually see that the numbers are the exact same that they are in the system of equations over here. In this system of equations, we had 2 equations, and those things just became our 2 rows of our matrix. We also have three numbers in the columns, 2 for the coefficients and then one for the constants over here. Those three numbers really just became our 3 columns over here. So really, it's just a way to represent this information that's in the system just in a different way. Alright? And when you do this, when you have a system of equations represented as a matrix, it's called an augmented matrix. That's just a sort of fancy word that you'll see in your textbooks and here in your classes. That's all that really means. Alright? So all we're really doing here is we're just sort of copying over the coefficients into this matrix, and we're sort of leaving out the variables. So we have -72. That becomes -72. Then we have this -3 and one two. That's -3 and one two. And then this -4 and 13 just becomes -4 and 13. So we're just copying over all the numbers, but we're just leaving out the coefficients. Because in a matrix, it's understood that these columns mean x and y coefficients. Now what you'll also see is you'll see this little black bar that's inside of these matrices, and this just means an equal sign. That's kind of what that means. So you'll see here that really, a matrix is just a more compact way to represent all of the information that was in the system of equations. Alright? That's really all there is to it. Later on, we'll learn different ways to manipulate matrices and even do some operations with them. But for now, all we need to do is basically just turn a system into a matrix. Let's go ahead and take a look at an example problem here. So we're going to take this 2x plus 3y. So we're going to take these system of equations and represent this as a matrix. So we've got 2x plus negative 3y plus z equals negative 4. And then we got 6x plus 3y equals 13, and then y minus z equals 8. Alright? So it's really important that you actually lay out when you have a system of equations so that you have the coefficients and the variables that are on top of each other, x's with x's, y's with y's, and z's with z's. And so that's one of the things you may have to do before turning something into a matrix. Alright? But remember, really, all we're going to do is we're just sort of going to extract out the coefficients. I'm going to have 3 columns here because I have 3 variables. Actually, I'm going to have 4 columns because I have 3 variables plus one constant on either side. So this is going to be like, the constants over here. Alright? So if you look at this first equation, what happens is I have a 2 in the x, negative 3 in the y, and then 1 in the z. So this is just going to be 2, negative 3, and then 1. The constant that goes on the other side is going to be negative 4. Alright? So that's for that first equation. Let's take a look at the second one. The second one has 6 in the x, 3 in the y, so 6x3y. But what about the z components? Here, we had one z over here. What happens if we just see nothing? Well, really, if you ever just see a blank space, it actually just means that there is, like, 0z there. There's, like, 0 there. So you don't just leave the matrix empty. You actually will just put a 0 there. Alright? So this will be 13. And then finally, what we're going to have is y minus z is 8. So here now what happens is that we have no x components. There's no x coefficient, so we just label that as 0. Then we have here as 1, and then minus z means negative 1. And over here, we have 8. So this is how you take this system of equations here and represent this as a matrix. So this would be the augmented matrix for this system of equations. Alright? That's it for this one, folks. Thanks for watching. I'll see you in the next one.

Write the equations in standard form, then represent the system using an augmented matrix.

$3x+5y-9=0$

$8x=-4y+3$

• A.
• B.
• C.
• D.

Write the system of equations represented by the augmented matrix shown.



• A. $x+2y+3z=5;5y+4z=1;4x+7y=12$
• B. $x+2y+3x=5;5x+4y=1;4x+7y=12$
• C. $x+2y+3x=5;5y+4z=1;4y+7z=12$
• D. $x+2y+3x=-5;5y+4z=-1;4x+7y=-12$

Performing Row Operations on Matrices

Welcome back, everyone. So back when we studied systems of equations, we saw lots of different ways to manipulate those equations. For example, we saw that we could swap the positions of 2 equations. We could also multiply equations by some number, like when we did the elimination method. We can also add equations together once we had those coefficients to be equal and opposite. Well, remember that a matrix is really just a representation of a system of equations. It's just 2 ways of writing the same information. So just as we did operations to these types of equations, we can also do operations on the rows of a matrix because remember, an equation is really just a row on a matrix. So we call these things row operations. What I'm going to show you in this video is that there are really just 3 of them that you need to know, and I'm going to break it down for you, showing you a bunch of examples. Alright? And there's also some new notation we'll learn as well. Let's get started with the first one, which is swapping 2 rows. This is by far the easiest operation, and it sounds exactly like what it sounds like. Right? We're just going to be swapping the position of 2 rows just like we swap the position of 2 equations. So, here, all that happens is that we had -1, 2, and 9 on the top row, and now it just goes to the bottom. So this is -1, 2, and 9. And then the 2, 6, and 12 that was on the bottom, now it just goes to the top, 2, 6, and 12. Now you'll see some notation for this written in your textbooks with some little r's and big R's. Really, all this stuff says is little r means the old row, and big R means the new row once you're done doing that operation. And the subscripts just tell you which number or which row they're talking about. So, for example, this is little r one over here, and that little r one becomes big R two and vice versa. This little r two becomes big R one. So that's really all that's going on there. It's just showing you old versus new and the number of the row that it is. Alright? So that's the first one.

Let's take a look at the second operation, which is multiplying one row by any non-zero number. Alright? So when we dealt with the system of equations in the elimination method, we could multiply an equation by some number. So, for example, we multiply this by 2. And what happens is we change all the coefficients. This would be -2x, and this would be 4y, and this would be 18. Well, we can do the exact same thing to the rows or the numbers in the rows of a matrix. So really all this is is we're going to take this little r two over here, and the notation for this is we're going to take little r two multiplied by 2, and that becomes now big R two. We're just going to rewrite this new row. Alright? So what happens is we're going to take all these numbers, multiply them by 2. This may end up being -2, 4, and 18. Notice how all these numbers are the same because remember, this matrix is just representing the system of equations. Alright? Alright. So these numbers here are all the same. Alright. So, let's move on to now the last one, which is just adding some multiple of one row to another. Alright. So when we did this for systems of equations and we finally got their coefficients to be equal and opposite, we could add the equation straight down and cancel out or get rid of 1 of the variables. What we were left with is we were left something like 10y equals 30. So now what we can do here is, with a matrix, we can do the same exact thing. Now when we did the first system, we always delete or not even rewrite that first equation because we're only just worried about that one equation here. With the matrix, you can't just sort of delete a row, so you just rewrite it. Right? So the 2, 6, and 12, you just rewrite the 2, 6, and 12. Alright? But now what you're going to do here is you're going to take this little r 2 You're going to take this little r 2, and I'm just going to add it to all the other numbers in little r one, and I'm just going to add these things straight down. And that now becomes my big R 2. So this should become 0, 10, and 30, and you're going to get exactly the same sort of numbers that you get on left and right. It's just another way to represent this system of equations. Now, unfortunately, this step here of adding some kind of a non-zero multiple of one row to another is actually, unfortunately, the most common step, so it's good to get some good practice with this. I also want to mention one other thing here. The last two steps that we talked about are operations, the multiplying and adding. They only affect one row. It's the row that they're you're currently doing an operation on. The only time you're actually doing 2 rows or you're affecting 2 rows is when you're swapping them. So what you'll see here is that we rewrote, for example, the 2, 6, and 12. We changed we never it never changed the entire time. And that's because the only row that was changing was row 2. Alright? So, anyway, those are the 3 operations. Let's go ahead and get some more practice here using, this sort of more complicated matrix. So here we've got 2, -6, 4, 10. We've got this big matrix over here. Let's take a look at the first one. The first one says we're going to take row 2, and we're going to swap it with row 3. So remember, this is just the notation for swapping. So all we're going to do here is this is going to be my r 2. This is going to be, sorry. This is going to be that's going to be r 2, and now it's just going to trade places with the 3rd row. Alright? So just going to rewrite this matrix over here. Remember, this the first row is going to remain completely unaffected. So this is 2, -6, 4, 10. Just rewrite it. Now what happens is the 3 eights, -7, and 0, will actually go to the bottom. 3, 8, -7, and 0, and now what happens is this row over here will go to the top. So this is going to be -1, 5, 9, and 3. Alright? So that is how you swap 2 rows. Alright? So now we're going to see here that this is our 3, and that was r 2 before. Let's take a look at the second one. So the second one says we're going to take r one. We're going to multiply it by a half, and then that's going to become the new r1. So this is really just multiplying something by a non-zero number. I actually want to point that out real quick here. You can only multiply by a non-zero number. You can't just multiply everything by 0 because it'd basically just be like almost deleting the equation. So you just can't do that. Alright? So let's take a look here. We're going to take this row 1, and then that's going to become the new r one. So what we can see here is that, remember, the rows the 2nd and third rows will remain completely unaffected. So those won't change at all. This would be 3, 8, -7, and 0, and this would be -1, 5, 9, and 3. So, that's what this b for b. And then what happens is for this row on the top, we're going to take all these numbers, and we're going to multiply them by half. So 2 becomes 1, the -6 would become -3, 4 become 2, and then the 10 would become 5. So this is what this new equation or matrix would look like. All right. So that is multiplication. The last thing we'll do is we'll do the addition. So we have that r two. We're going to add it to a multiple of r three, and that's going to become my big R 2. Alright? Let's take a look at this. So remember, what's going to happen here is the row 2 is going to get rewritten, which means that we can just rewrite the 1st and third rows. So in other words, we can just do the 2. By the way, we're not carrying over the changes that we made in a and b. This is going to be 2, -6, 4, and 10. And this is going to be, -1, 5, 9, and 3. So what's going on with this middle row over here? Well, remember, what this whole process is by adding one row to another, you're going to take all of these numbers here in row 2, and you're going to add them to 3 times all the numbers that are in row 3. Alright? So, actually, I should mention this is here r 3. So, basically, I'm going to take all these numbers here and multiply them by 3 and then add them to all these numbers over here. Alright? So this is how this is going to work out. We're going to come up with 4 numbers. Right? So this is going to the first one's going to be 3 +3 times -1. That's this pair over here. 2nd number is going to be 8 +3 times 5, just this row or this column. And the 3rd number is going to be -7 +3 times 9, which is going to be this pair. And then finally, you have 0 plus 3 times 3. Hopefully, you guys get the pattern. Right? So, basically, we're just going to go ahead and calculate all of these. And remember, this is just to do this operation over here. So this works out to 3 +- three, which turns out to just be 0. So this is going to be 0. This is going to be 8 +3 times 5, which is 15. That's going to be 23. That's the second number. The third one is going to be -7 plus 3 times 9, which is 27. That works out to positive 20. That's positive 20. And the last number is going to be 0 plus 3 times 3, which is just 9. Alright? So that's how to do these kinds of operations, where you are adding 1 row to another. Hopefully, that made sense. Thanks for watching, and I'll see you in the next one.

Perform the indicated Row Operation.

SWAP $R_1\leftrightarrow R_2$

• A.
• B.
• C.
• D.

Perform the indicated Row Operation.

ADD $R_1+2\cdot R_3\rightarrow R_1$

• A.
• B.
• C.
• D.

Solving Systems of Equations - Matrices (Row-Echelon Form)

Welcome back, everyone. So in the last few videos, we've learned the row operations that you can do to the rows of a matrix, like swapping, multiplying, and adding. And I mentioned that we would eventually use those to solve the system of equations. Well, that's exactly what we're going to do in this video. We're going to solve the system of equations by getting a matrix in a very particular form that we'll discuss in just a second. The whole idea is that I'm going to take a system of equations, turn it into a matrix, and then use row operations to get a very particular pattern of numbers of ones and zeros. And then once I get that, I can turn it back into a system of equations and then solve it that way. Let's go ahead and take a look here. The first time you see this, it might be kind of intimidating, but I'm going to break it down for you, and we'll work out this example step by step. Let's get started here.

So, the whole idea is that we're going to use these row operations to get a matrix with ones along the diagonal. So, notice how I have this sort of diagonal here from top left to bottom right, and then I have zeros underneath the diagonal. That's really what you're trying to get, ones along the diagonal and zeros underneath. Now remember, what happens is that these coefficients really just stand for the numbers here stand for the coefficients of a variable, in a system of equations. So, the reason you want to get to this in this form, which is, by the way, called row echelon form, is because once you turn it back into a system of equations, then really what happens is that you're just going to get equations that you can substitute, and then solve for 'x' and 'y' using that method. So, it really just turns into a regular system of equations problem, which we've seen how to solve before. I want to mention here, by the way, that these numbers can actually be anything. There's no restrictions on them, so they don't have to be ones and zeros or anything like that.

Alright, so what I'm going to do is I'm actually going to break this example down. We're going to work this out together. I'm going to show you step by step how we get to this row echelon form. Alright? Let's take a look. So I've got my system of equations over here, –x + 2y = 4, x + 7y = 14. In fact, it's actually exactly the same system of equations I had over here. So, I'm really just going to start by turning it into a matrix and copying this over. So I've got my augmented matrix over here. Alright, remember, the whole goal is I want to get ones along the diagonal and zeros everywhere else. Here, I've got a negative one and seven along the diagonal, so I'm going to need to get a one in this position. And that actually brings me to the first tip here. I'm going to give you some tips for solving these types of problems, and the first one is just to go row by row and work your way top to bottom. Alright, just work one at a time, focus on one number, and just generally try to go from top to bottom like this. So let's try to get a one in this position over here. How would we do that? Well, to do that, we're going to have to look at our row operations again: swap, multiply, or add. Let's consider each one of them. Can I swap two numbers over here to get a one in this position? Well, actually, you can because notice how this is a negative one and positive one. So if you swap these 2 rows, then you'll get a one there. So that's the first thing you can do. You won't always have to do that, it's just, in this case, we can swap because we've seen that there's a one in this position. So we're going to swap row 1, and that will just become my new row 2. So, really, all that happens is that these rows just switch places. So this is 1, 7, and 14 now, negative 1, 2, and 4. And now, all of a sudden, we can see that we have a one in this position. That's one of our numbers. Alright? So now we just have to focus on these two numbers. This has to become a zero, and this has to become a one. We're going to use row operations to do it.

So you might be thinking that, well, we'll just stick with trying to get the ones along the diagonals. So might be thinking, well, it just doesn't matter. I can just focus on this one. But actually, what I'm going to show you here is that trying to get this one isn't going to be the right move. Because what happens is if you try to get this position here to be a one by multiplying this equation by, let's say, 1 half, then this will become a one, but this will become negative 1 half. And you're going to end up with a weird negative fraction here. Then later on, to try to get rid of it, you're going to have to mess up the one that you've already gotten. So instead, what happens is that kind of brings me out to my second tip. Whenever you get a one along the diagonal, you would actually want to get everything underneath it to be a zero before you move on and try to get to the next one. What do I mean by this? Now that we've gotten this first one, I'm going to focus on getting this number to be a zero before I focus on getting this to be a one. And we're going to see why that works in just a second. So how do I get this one to be a zero? Well, can we swap? Well, swapping is going to be pretty silly because we're just going to undo all the progress we've already done here. So that's not going to work. So what about multiplying? Well, the only way we could get a zero out of this is if I multiply the entire row by zero, but I can't do that because I have to multiply rows by non-zero numbers. So multiplying isn't going to work either. The only way to get a zero in these types of problems is you're going to have to add. By the way, this is always going to happen. So to get zeros, you're going to have to always add something. Alright? So here, what we're going to do is we're going to take row 2. We're going to have to add it to something to get a zero in this position. What do I have to add to this to get it to cancel out to zero? I just have to add one. And that's exactly what I have in the first row. So remember, I can multiply or I can add a multiple of a row. But, in this case, all I have to do is just add row 2 and row 1 together with no multiple, just 1 times row 1. And that's going to be my new row 2. Alright? So now what happens here is, remember, that row operation will only affect row 2, so row 1 will remain completely the same: 1, 7, and 14 doesn't change. Now what happens here is I'm going to add these coefficients down. 1 and negative one becomes zero, 7 and 2 become 9, and then 14 and 4 become 18. Now if you see what happens here, I've got a one in this position, and I've got a zero underneath it. So that's good. I've gotten two of my numbers. I really only have one thing to do left, and that's I have to turn this thing into a one.

Alright, so how does that work? Well, whenever you're trying to turn numbers into ones, you're not going to add. You're going to actually multiply. Because now what I can do in this problem is I can multiply this whole entire equation here by whatever I need, to get this to be a one. And I really just have to multiply this entire equation here by 1/ninth. So what I'm going to do is I'm going to multiply, 1/ninth times row 2. Now the reason this is helpful is because notice how multiplying this equation won't actually affect the zero because 1/ninth times zero is still zero. So this is why multiplying to get ones is going to be easier. So here what happens is this is going to be 1, 7, and 14, and this is going to be zero. So I've got zero over here. This becomes a one. And then if I multiply 18 by 1/ninth, that actually will become a two. So now if you look at this, I've got ones along the diagonal, and I've got a zero underneath the diagonal. So this is now in row echelon form. So that's what this means here. And now that we're done, we can turn this back into a system of equations and solve. What we're going to see here is we have x + y = 14, which is actually one of our original equations. And then we have 0 + y, this is just 1y, equals 2. So one of our variables is now already solved for. We have y = 2. And now all you can do is just plug this back into this equation, this 2, using substitution, and then you'll get the x value. And if you actually do that, what you're going to see here is that x + 7 times 2 equals 14. And what you're going to see here is that x is equal to zero because these things will actually end up canceling out. So this is also sometimes called back substitution in your problems. That's really what this means, is that you'll use row operations to get a matrix, and then you can just sort of backwards substitute to get your answers.

But that's really all there is to it. We use the row operations, work one at a time to get row echelon form, then turn it back into a system of equations which we've seen how to solve. That's really all there is to it, folks. Now one thing I want to mention here, by the way, is that this method of solving systems is sometimes called Gaussian elimination. So if you ever see that, that's what that means. Thanks for watching, and let's get to some practice.

Example 1

Hey, everyone. Welcome back. So in this problem, we're going to take this system of equations that we have given to us right here, and we're going to solve it using row operations. And the key thing here is, remember, when we use row operations, we're trying to get a matrix in row echelon form. And remember what that looks like. Row echelon form means that we have a matrix with all ones on the diagonal, and we have all zeros under the diagonal. And remember that these numbers over here that are sort of above and to the right of the diagonal can be anything. There's no restriction on them. So, we're going to have to take this system of equations and turn it into a matrix first so that we can start doing that. Let's get started here. The first thing is we're going to convert this into a matrix. And, really, we've done this before. We just have to pull out the coefficients. So this is going to be 1, 3, 4, and 2. This will be 2, 5, 7, 9, and then 4, 8, 10, and then this is going to be 14. Alright? So if you look here, I've already actually gotten one of the numbers that I need. I've gotten one of the ones on the diagonal, so it's a little bit of a head start, which is good. Now, what we have to do is we have to focus on these numbers. I want these to be ones, and then I want these numbers, the 2, 4, and the eights. I want those things to become zeros. And how do I do that? I'm going to have to use all the row operations that we've learned in order to get that system of equations or that matrix in row echelon form. Let's go ahead and get started here. Now you might think that you should focus on any number. Like, for example, you could focus on this 5 or the 10. But remember that second tip that we discussed in the video. Obviously, you always want to work down sort of from top to bottom in your equations, but you also every time you get a one, you want to make sure that you get all these numbers to be 0 underneath the diagonal, or underneath that one before you start focusing on the next one. What happens is if you try to make this one, then you're going to affect this cell over here, this number. And then later on, you're going to have to sort of get this to be 0, and then you're going to have to sort of mess up the one that you've already gotten. So it's always better to get this thing to be 0 or these numbers to be 0. Let's go ahead and do that. Alright? So, how do I get this number to be 0? Well, I can't swap because nothing was going to get me a 0 in that place, and I can't multiply this thing. I have to multiply this whole entire equation by 0. So, The only thing I have to do is the only thing I can do is I can add. So I'm going to have to add something to row 2 in order to make it 0. So, how do I do that? Well, the only number that's going to make this 0 is if I multiply or if I add it to negative 2. So I'm going to have to add so row 2 to some multiple of some equation in order to get a new row 2, and that's going to give me a 0. Now, one of the reasons it's really nice to get ones in these equations is because then you could just multiply them by a number, to get something to cancel out with this number over here. So, for example. So I've got this 2. I need it to cancel out by becoming by adding it to negative 2. So what I can do is I can take this whole entire row, and I can multiply it by negative 2. So I'm going to do negative 2 times row 1 and then add it to row 2, and that's going to become my new row 2. Let's work it out real quickly and just see how this works. So, this row 2 that I have is just equal to 2, 5, 7, and 9. Right? That's what that row is. What about negative two times row 1? Take all the numbers that you see over here and multiply them by negative 2. What do you get? I'm going to get negative 2, and I'm going to get negative 6, and I'll get negative 8, and then negative 4. Alright. So you multiply all those numbers. Now what happens is when you add these 2 rows, what you'll see is that the 2 and negative 2 will cancel, leaving you with just 0. The negative 6 and 5 becomes negative 1. Negative 8 + 7 becomes negative 1, and the negative 4 + 9 becomes 5. So this over here is actually what your new row 2 is. Alright? So now let's go ahead and rewrite this matrix. And remember, the only thing that gets affected here is just this row 2. So let's rewrite this. So this is going to be it's going to be 1, 3, 4, 2. And then remember, the 3rd row is going to be unaffected, so 4, 8, 10, and 14. But now the 2nd row gets rewritten. So 0, -1, -1, 5. Alright? Now if you look here, we've actually made some progress. I've got a one here, and then I've got a 0 over here. So it's making some progress. And if you actually look, this number is really close to being the one really close to being the one that we need along the diagonal, but it's negative. But we'll focus on that later. Remember, what we also want to do is we want to keep on working down the equations and getting all the numbers underneath the ones to be zeros. So now let's take a look at this third equation. You actually see that we're going to do something very similar. I'm going to have to get this to be a 0, so I can't swap it. Otherwise or I could swap it, but then I'm going to have to deal with the row that I just messed up, and so that's not going to be a good idea. I can't multiply this, so I'm going to have to add it to something. I'm going to have to add something to row 3 in order to get these numbers to cancel. So I'm going to add row 3 to something. Now just like I multiplied the first equation by negative 2 to cancel out the 2 that was here, I can do the exact same thing. I can instead multiply row 1 by negative 4, so then I'll get a negative 4 that cancels out with a positive 4.

Example 2

Welcome back, everyone. So let's take a look at this example. Again, we've got these three system of equations, and we want to solve this, which means we want to find solutions for x, y, and z. The way we're going to do this is by writing a matrix in row echelon form. Remember, that's just that specific format where we have ones along the diagonal and zeros everywhere else. Let's go ahead and get started here. The first thing we have to do is convert this into a matrix just by pulling out all the numbers and coefficients. So this is going to be a 2, 4, 6, and then 24. This will become a 1, 5, 12, and then 60, and this will become a 3, 6, 15, and then 20. So remember, all we have to do is just work the equations from top to bottom, focus on one number at a time. Every time we get ones, we're going to try to focus on everything else, getting them to be zeros. So let's take a look at this first number here. I just want a one that's in this position. I've got a 2 there, so that's bad. So can I use any of my operations like swapping, multiplying, or adding to solve this? Actually, I can. So what you'll see here is that I can actually swap these two rows in order to get one in that position. So the first thing you can do is just swap. So we'll swap row 1 and row 2, and they'll basically just become each other. Alright? So, in other words, I'm just gonna rewrite this matrix, and this is gonna be 1, 5, 12, and then I've got 60. And this is gonna become 2, 4, 6, and then 24. And then I've got 3, 6, and then 15. And then finally, I've got 20. Alright? So I've gotten one of my numbers already. I've got 1. Now remember, rather than focusing on these other numbers and getting them to be ones, the next thing you wanna do is focus on getting everything underneath those ones to be zeros before you move on to the next one. So the way we do that, remember, is by adding. So what we're gonna do is, we're gonna take something to this row over here. And in order to cancel out this 2 to become a 0, I have to add it to something else. I can't add it to 3 because those things aren't gonna cancel out to 0. But what I can do is I can add row 2, and I can add it to a multiple of row 1 because I have this thing as 1 over here. So I can do this by multiplying row 1 by negative 2. And that will become my new row 2. Let's work this out real quick. So my row 2 is equal to, again, 2, 4, 6, and then 24. And then if I multiply negative 2 times row 1, that equals remember, I just multiply all these things by negative 2. So this is going to be negative 2, this would be negative 10, this will be negative 24, and this will be negative 120. Alright? Now, once you add those two things, what do you get? These things will cancel, and you'll just end up with 0, negative 6, and this would be negative 18, and this would be negative 96. Alright? So now that becomes my new row 2, and so you can just rewrite this matrix. So, really, what happens is I just get, 1, 5, 12, and 60, then the 3, 6, 15, and 20, because those things remain completely unchanged. And now the only thing that changes is row 2, which is now 0, negative 6, negative 18, and then negative 96. Alright? Notice how we got a 1, and now I've got one of my zeros. Now I'm just gonna focus on getting this thing to be 0, and I'm just gonna do a very similar step. Instead of adding something to row 2, I'm gonna add something to row 3. And so I'm gonna add row 3. And just like we added a multiple of row 1, we're gonna do the exact same thing. But instead of negative 2, all we're gonna do is we're gonna multiply or add to a multiple of negative 3 of row 1. Alright. So it's the same exact procedure, just trying to cancel out that 3 there. So what does this become? Well, row 3 again is just equal to I've got 3, 6, 15, 36, 15, and 20, and then negative 3 times row 1 equals I'm gonna have negative 3, This becomes negative 15, negative 36, and then negative 180.

Solving Systems of Equations - Matrices (Reduced Row-Echelon Form)

Welcome back, everyone. So in another video, we learned how to solve a system of equations by using something called the row echelon form. We wrote a matrix in a specific form where we had ones along the diagonal, and then we had zeros everywhere else. What I'm going to show you in this video is another way of solving a system of equations by writing a matrix in something called reduced row echelon form. Now it might seem like this is an entirely new process, but I'm actually going to show you it is really similar to this. We're going to use all the same steps and row operations and all of that stuff. And then we'll just actually work out this example here. So let's go ahead and get started. Really, the main difference between these types of forms here is the matrix that you're trying to work towards. With row echelon form, we had ones along the diagonal, and we had zeros under the diagonal like we have over here. And for reduced row echelon form, what you're trying to get is ones along the diagonal. So that's exactly the same, except you're trying to get zeros under and above the diagonal. So you see that's really the only difference here. And remember, these numbers can be anything. There's no restrictions on them. The key advantage of getting something in this format over here is that when we turn it back into a system of equations, you're done. You actually don't have to do any more work versus with the row echelon form, once we converted something to equations, we had to use substitution to get your x and y values and things like that. With this form, you actually have no more work to do. So what I'm going to do in this video is we're actually just here to sort of look at the example from the last video. We're going to sort of pick up from there.

So what I mean by that is that in this example, we used this matrix with 1, 7, 14, -1, 2, and 4, and we used our different row operations like adding and multiplying. And then when we got to this point over here, we had row echelon form because we had ones and zeros. And then we turned it back into a system of equations. And what we got here was that the answer was y equals 2 and x equals 0. So we're going to sort of pick up from this step, and we're just going to go one step further because now what we have to do is get something in reduced row echelon form. So I have ones along the diagonal, zeros under, but now I'm going to have to figure out how to get this position to be a 0 because that would make it reduced row echelon form. Alright? So that's really all there's to it. We're actually just going to sort of pick up from this step, and we're going to have to do just one more sort of round of swapping, multiplying, and adding, and things like that. And what we should expect is we'll get the same exact answer. Alright? Let's get started here.

So remember, I've got this matrix. I've got 1, 7, 14, 0, 1, 2. So I've got these numbers already that are good, and then I just have to get this number over here to be a 0. How do I do that? Well, let's take a look at our row operations. Can I swap? Swapping isn't going to help here because that's going to mess up all the ones and zeros you already have. Can I multiply this equation by something to get this to be 0? You can't because the only thing is you would have to multiply this whole thing by 0, but you can't do that. So remember, the only way to get zeros in a position is you have to add. So we're going to have to add something to this equation over here to cancel out that 7. So we're going to have to add something to row 7 over here to cancel this out. What do I have to do? Well, if you take a look here, I've got 7. The only way to cancel it out is if I have -7. So remember, I can add a multiple of row 2 to cancel out this 7 over here. And what you have to do is you have to multiply this whole row 2 by -7. Multiply -7 times this number, it'll then cancel out this positive 7. This is going to be -7 times row 2. Alright? Now let's go ahead and work this out here. What does that turn out to be? Well, what happens is row 2 is completely unaffected, so this would be 1, 0, 1, and 2. What does row 1 become? This becomes 1 since adding -7 times 0 is still just 1.

This is going to be 7 + (-seven times 1), and that's actually going to cancel out to 0. And then what about this 14? This is going to be 14 plus -7 times 2, which ends up being 0. So what you're actually going to see here is that this completely just cancels out to 0. This won't always happen, by the way, so this won't always just be 0. Sometimes you'll get other numbers, but in this particular case, that's what it worked out to be. So now what you'll see here is that we have this matrix in reduced row echelon form. I got ones along the diagonal and zeros everywhere else. So this is reduced row echelon form. And when you convert it back into a system of equations, we're going to see what happens here. With the x coefficients, I have 1 x. And then with the y coefficients, I have 0 y. So it's almost like it just doesn't exist. And this equals 0. So in other words, x equals 0. And then for the bottom row, the second row, this is 0 x, so that goes away, plus 1 y equals 2. In other words, that just ends up being y equals 2. These are exactly the numbers that we got when we did it using the Gaussian elimination or row echelon form, but we did it in sort of a slightly different way. So we got the same exact answers, and that's good.

So, to summarize, the key difference between these two different types of methods is how much work you have to do between the matrices and equations. With row echelon form, you have to do less work with the matrices, but then you'll have to do more work when you turn it back into equations. Whereas with reduced row echelon form, you're going to have to do more work with the matrices upfront. So you're going to have to do more row operations, but then you're going to have to do less work when it comes down to the equations. And it'll actually just sort of spit out your numbers right for you. Alright? So one last thing to point out here, this is sometimes called Gaussian elimination, this method here of row echelon form, whereas this one that we're working with is sometimes called Gauss Jordan elimination for the mathematicians that devised them. But that's really all there is to it. Thanks for watching, folks, and I'll see you in the next video.

Solve the system of equations by using row operations to write a matrix in REDUCED row-echelon form.

$4x+2y+3z=6$

$x+y+z=3$

$5x+y+2z=5$

• A. $x=0,y=-3,z=4$
• B. $x=-\frac14,y=-\frac{19}{4},z=\frac{11}{2}$
• C. $x=1,y=4,z=-2$
• D. $x=\frac12,y=\frac12,z=1$

Here’s what students ask on this topic:

What is a matrix in algebra?

A matrix in algebra is a rectangular array of numbers arranged in rows and columns. It is used to organize and represent data, especially in systems of equations. Each element in a matrix is identified by its row and column position. For example, a 2x3 matrix has 2 rows and 3 columns. Matrices are useful for performing various operations such as addition, subtraction, and multiplication, and they play a crucial role in linear algebra and other advanced mathematical topics.

How do you convert a system of equations into an augmented matrix?

To convert a system of equations into an augmented matrix, follow these steps:

1. Write down the coefficients of each variable in the system of equations, aligning them in columns.
2. Include the constants from the right-hand side of the equations as the last column.
3. Separate the coefficients and constants with a vertical line to indicate the augmented part.

For example, the system:

$\{\begin{array}{c}\mathrm{2x}+\mathrm{3y}=5\\ \mathrm{4x}-y=3\end{array}$

becomes the augmented matrix:

$\left[\begin{array}{c}23|5\\ 4-1|3\end{array}\right]$

What are the three main row operations on matrices?

The three main row operations on matrices are:

1. Row Swapping: Interchanging two rows in the matrix.
2. Row Multiplication: Multiplying all elements of a row by a non-zero scalar.
3. Row Addition: Adding a multiple of one row to another row.

These operations are used to manipulate matrices into simpler forms, such as row echelon form or reduced row echelon form, which are useful for solving systems of equations.

What is row echelon form?

Row echelon form (REF) is a form of a matrix where:

1. All non-zero rows are above any rows of all zeros.
2. The leading entry of each non-zero row after the first occurs to the right of the leading entry of the previous row.
3. The leading entry in any non-zero row is 1.

This form is useful for solving systems of linear equations because it simplifies the process of back substitution.

What is the difference between row echelon form and reduced row echelon form?

The main difference between row echelon form (REF) and reduced row echelon form (RREF) is:

• Row Echelon Form (REF): Has ones along the diagonal and zeros below the diagonal. The leading entry in each non-zero row is 1, and each leading 1 is to the right of the leading 1 in the row above it.
• Reduced Row Echelon Form (RREF): In addition to the properties of REF, RREF has zeros above and below each leading 1. This form provides a direct solution to the system of equations without further steps.