Hey, everyone, and welcome back. So in the last video, we got introduced to this idea of conic sections. Basically, various ways you could slice a three-dimensional cone with a two-dimensional plane to get different shapes. Now today, we're going to be looking at the first shape, which is the circle. And you can get a circle from slicing a three-dimensional cone directly horizontally. Now, I think a circle is a pretty general shape that we're all familiar with. What we're going to be looking at in this video is how the equation for a circle will justify both the size and position that that shape is in. Now that might sound a bit complicated and a little bit scary, but don't sweat it. Because in this video, we're going to be taking a look at some graphs and examples that I think are going to make this concept super straightforward. So let's get right into this.
Now the thing that makes a circle unique is that a circle contains all points which are the same distance from the center of the circle. To understand this, let's say you're looking at a circle and you have the center of it. If you want to get to this point right here on the circle, this would be the same distance as going to this point or going to that point. It's the same distance all the way around, and that's what makes this shape unique.
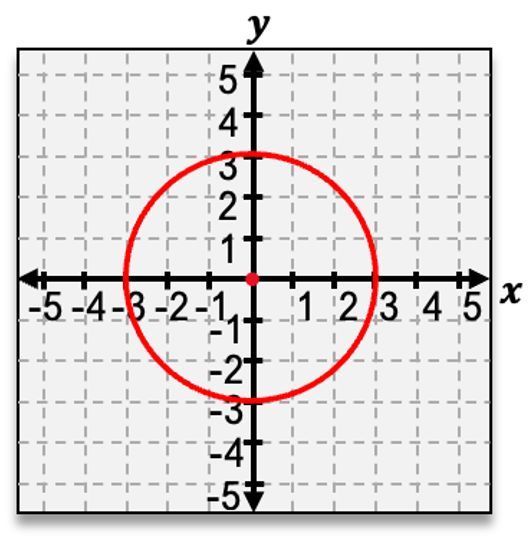
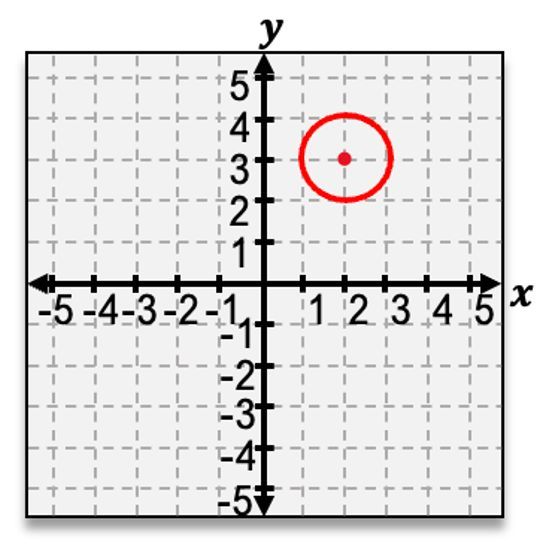
Now, in order to graph a circle, there are two things you need. You need the center and you also need this distance we just described, which is called the radius. Now, if you're given the graph already it's actually pretty straightforward to find both of these. So if you want to find the center of a circle, let's say you're dealing with a circle that's at the origin of your graph. This is a pretty common case, and when this happens the center of your circle is going to be at (0,0). This is what it means to be at the origin. Now to find the radius of the circle, well, we could just start at the center and count. It takes 1, 2, 3, 4 units to get to this point, and so that means our radius is 4.
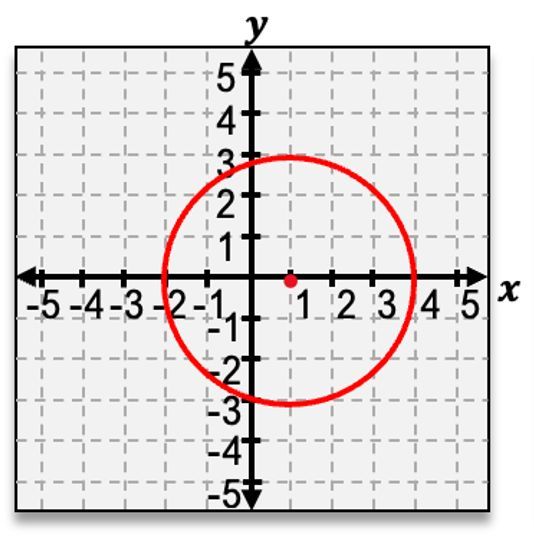
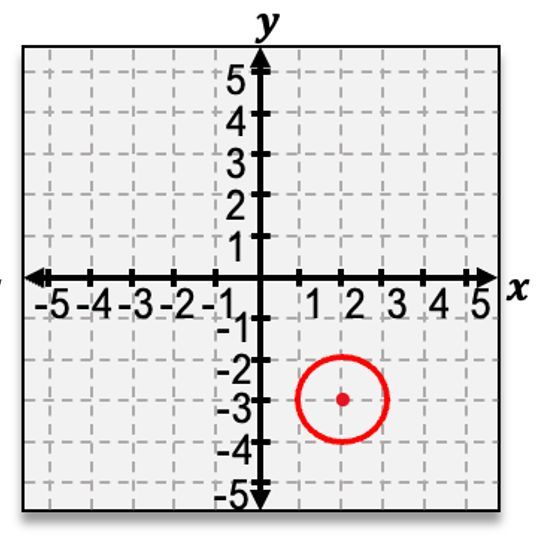
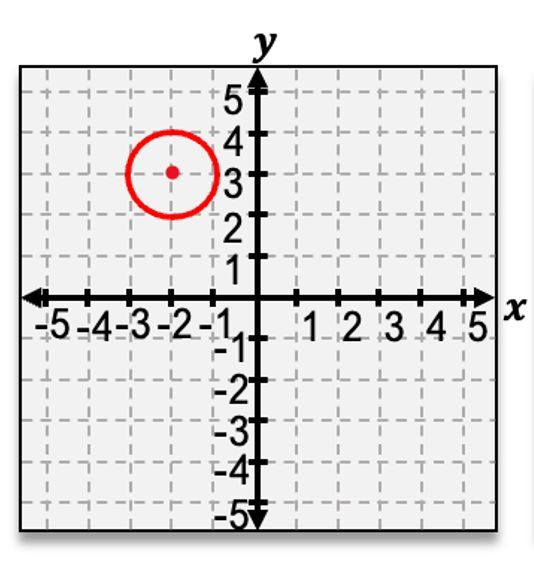
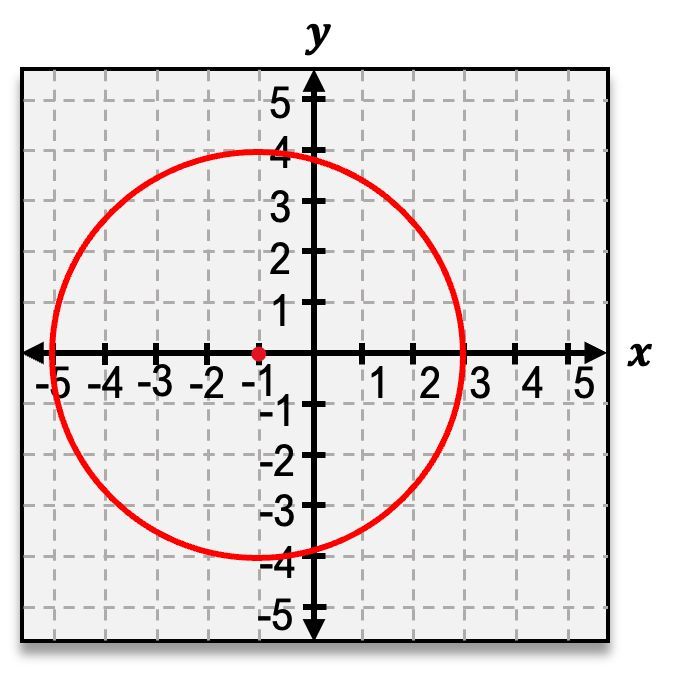
Now let's say we have a circle that this time is not at the origin. Well, when this happens, your first step should be to find where your new center,
But once you have these things, you can write the equation for the circle. If you have a circle at the origin, the equation is going to be
x2
+
y2
=
r2
. And the only thing we really care about in this equation is the
Now if the circle is not at the origin, the equation is going to look something like this. Notice it's very similar to what we had before except now we have a minus
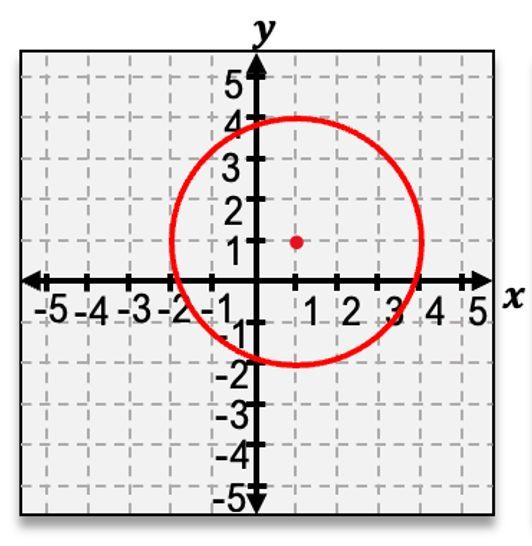
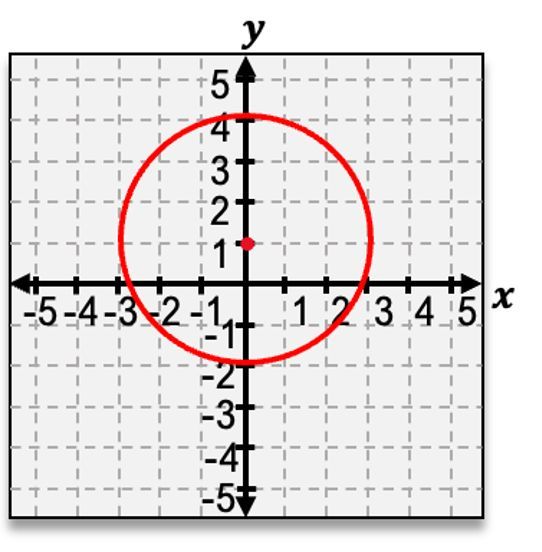
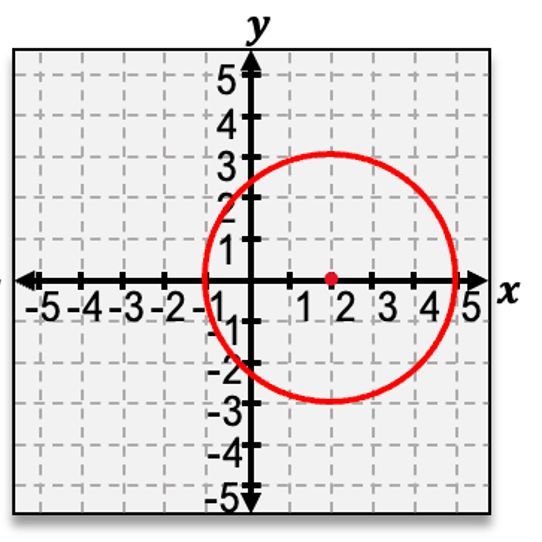
Now, something that I'll mention is that it's actually not too common that you're going to see the graph of the circle already given to you, but rather you're going to see the equation of the circle and have to graph it from there. So let's actually see if we can try an example where we graph a circle from just the equation. Now, our first step should be to
figure out what our center is
Now step 2 tells us to find the radius of our circle. Well notice for the equation this last term is
Now our third step says to plot 4 points which are a distance
Now one more thing that I wanna mention is that whenever you're dealing with a circle, the circle is not an example of a function. And this is because the circle would fail the vertical line test. We talked about in previous videos how if you're able to take a line and draw it on a graph, and that line crosses more than one point on the curve, this means you are not dealing with a function. And since the circle fails the vertical line test, it's not a function. So that's the basic idea behind the equations and graphs for a circle. Hope you found this video helpful. Thanks for watching, and let me know if you have any questions.