Circles: Videos & Practice Problems

Circles are defined as the set of all points equidistant from a center point, characterized by the radius. The standard equation for a circle centered at the origin is $x^2+y^2=r^2$, while for a circle not at the origin, it takes the form ${(}^x+{(}^y=r^2$. Converting from general to standard form involves completing the square for both x and y terms, ensuring accurate graphing and understanding of circle properties.

Circles in Standard Form

Conic sections are fascinating shapes formed by slicing a three-dimensional cone with a two-dimensional plane, and one of the most fundamental shapes is the circle. A circle is defined as the set of all points that are equidistant from a central point, known as the center. This unique property of circles allows us to describe their size and position using specific mathematical equations.

To graph a circle, two key elements are required: the center and the radius. The center is typically denoted as (h, k), where h represents the horizontal position and k represents the vertical position. The radius is the constant distance from the center to any point on the circle. For example, if a circle is centered at the origin (0, 0), the equation can be expressed as:

$$x^2 + y^2 = r^2$$

where r is the radius. If the circle is not centered at the origin, the equation adjusts to account for the new center, taking the form:

$$ (x - h)^2 + (y - k)^2 = r^2 $$

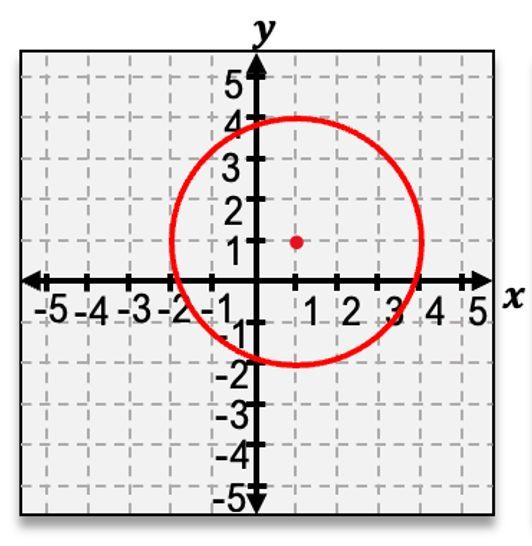
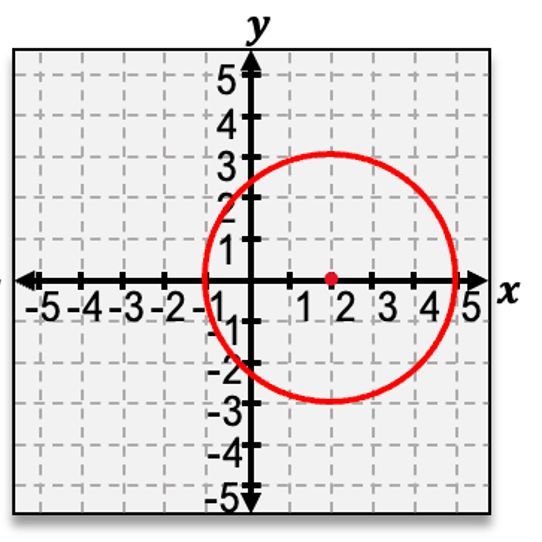
For instance, if a circle has a center at (2, 1) and a radius of 4, the equation would be:

$$ (x - 2)^2 + (y - 1)^2 = 4^2 $$

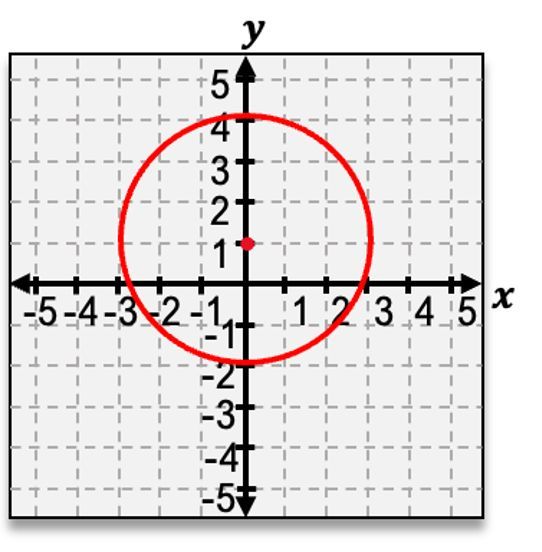
When given the equation of a circle, one can derive the center and radius to graph it. The center can be identified from the values of h and k, while the radius can be determined by taking the square root of the constant on the right side of the equation. For example, if the equation is:

$$ (x - 1)^2 + (y - 2)^2 = 9 $$

the center is (1, 2) and the radius is 3, since \( r^2 = 9 \) implies \( r = \sqrt{9} = 3 \).

To graph the circle, one would plot the center and then mark points at a distance equal to the radius in all four cardinal directions (up, down, left, right) from the center. Connecting these points with a smooth curve results in the visual representation of the circle.

It is important to note that a circle does not represent a function in the mathematical sense, as it fails the vertical line test. This test states that if a vertical line intersects a graph at more than one point, the graph does not represent a function. Since a circle can be intersected by a vertical line at two points, it is classified as a non-function.

Understanding the properties and equations of circles is essential in geometry and serves as a foundation for exploring more complex conic sections.

Sketch a graph of the circle based on the following equation: $x^2+{(y-1)}^2=9$

• A.
• B.
• C.
• D.

Answer: (D)

Sketch a graph of the circle based on the following equation: ${(x-2)}^2+{(y+3)}^2=1$

• A.
• B.
• C.
• D.

Answer: (B)

Find the equation for the following circle:

• A. $x^2+y^2=4$
• B. $\left(x+1\right)^2+y^2=4$
• C. $\left(x-1\right)^2+y^2=4$
• D. $\left(x+1\right)^2+y^2=16$

Answer: (D)

Circles in Standard Form Example 1

To write the equation of a circle, we use the standard form given by the equation:

\( (x - h)^2 + (y - k)^2 = r^2 \)

In this equation, \((h, k)\) represents the center of the circle, and \(r\) is the radius. Let's explore how to apply this formula through a few examples.

**Example A:** Consider a circle with its center at \((0, 1)\) and a radius of \(3\). Here, we identify \(h = 0\) and \(k = 1\). Plugging these values into the standard form, we have:

\( (x - 0)^2 + (y - 1)^2 = 3^2 \)

This simplifies to:

\( x^2 + (y - 1)^2 = 9 \)

**Example B:** For a circle centered at \((1, -2)\) with a radius of \(1\), we set \(h = 1\) and \(k = -2\). The equation becomes:

\( (x - 1)^2 + (y + 2)^2 = 1^2 \)

Which simplifies to:

\( (x - 1)^2 + (y + 2)^2 = 1 \)

**Example C:** Now, consider a circle with a center at \((-6, 3)\) and a radius of \(\sqrt{5}\). Here, \(h = -6\) and \(k = 3\). The equation is:

\( (x + 6)^2 + (y - 3)^2 = (\sqrt{5})^2 \)

This simplifies to:

\( (x + 6)^2 + (y - 3)^2 = 5 \)

In summary, to find the equation of a circle, identify the center coordinates and the radius, then substitute these values into the standard form of the circle's equation. This method allows for the accurate representation of circles based on their geometric properties.

Circles in General Form

In the study of circles, understanding the general form of a circle's equation is crucial for converting it to standard form. The general form of a circle's equation can appear daunting, but with the right approach, it can be simplified. The general form is typically expressed as:

$$x^2 + y^2 + Dx + Ey + F = 0$$

To convert this equation into standard form, which is:

$$ (x - h)^2 + (y - k)^2 = r^2 $$

where \((h, k)\) is the center of the circle and \(r\) is the radius, you will need to complete the square for both the \(x\) and \(y\) terms. The process begins by grouping the \(x\) and \(y\) terms together and moving the constant term to the other side of the equation. For example, if you have:

$$x^2 + 2x + y^2 - 4y + 1 = 0$$

you would rearrange it to:

$$x^2 + 2x + y^2 - 4y = -1$$

Next, you complete the square for the \(x\) terms. Take the coefficient of \(x\) (which is 2), divide it by 2 to get 1, and then square it to add 1. Do the same for the \(y\) terms, where the coefficient is -4. Dividing by 2 gives -2, and squaring it results in 4. You will add these values to both sides of the equation to maintain equality:

$$x^2 + 2x + 1 + y^2 - 4y + 4 = -1 + 1 + 4$$

This simplifies to:

$$ (x + 1)^2 + (y - 2)^2 = 4 $$

Now, you can identify the center of the circle as \((-1, 2)\) and the radius \(r\) as the square root of 4, which is 2. To graph the circle, plot the center and then move 2 units in all directions (up, down, left, right) to find the points on the circle. Finally, connect these points with a smooth curve to complete the circle.

This method of converting from general to standard form and graphing the circle is essential for solving problems related to circles in coordinate geometry.

Determine if the equation $x^2+y^2-2x+4y-4=0$ is a circle, and if it is, find its center and radius.

• A. Is a circle, center = $c\left(0,0\right)$, radius $r=2$.
• B. Is a circle, center = $c\left(0,0\right)$, radius $r=3$ .
• C. Is a circle, center = $c\left(1,-2\right)$, radius $r=3$.
• D. Is not a circle.

Answer: (C)

Determine if the equation $x^3+y^2+4x-8y+4=0$ is a circle, and if it is, find its center and radius.

• A. Is a circle, center = $c(0,0)$, radius $r=4$.
• B. Is a circle, center = $c(2,-4)$ , radius $r=4$.
• C. Is a circle, center = $c(-2,4)$ , radius $r=4$.
• D. Is not a circle.

Answer: (D)

Here’s what students ask on this topic:

What is the standard equation of a circle and how do you use it to graph a circle?

The standard equation of a circle is given as:

${\left(x,-,h\right)}^2+{\left(y,-,k\right)}^2=r^2$

Here, (h, k) represents the center of the circle, and r is the radius. To graph a circle, first locate the center point (h, k) on the coordinate plane. Then, use the radius to plot four points: one above, one below, one to the left, and one to the right of the center. Finally, connect these points with a smooth curve to form the circle.

How do you convert the general form of a circle's equation to the standard form?

To convert the general form of a circle's equation to the standard form, follow these steps:

1. Group the x and y terms together and move constants to the other side of the equation.
2. Complete the square for both x and y terms. For each, divide the middle term by 2, square it, and add it to both sides of the equation.
3. Factor the completed square terms into binomial squares.
4. Simplify the equation to obtain the standard form:

${\left(x,-,h\right)}^2+{\left(y,-,k\right)}^2=r^2$

This process allows you to identify the center (h, k) and radius r for graphing.

Why is a circle not considered a function?

A circle is not considered a function because it fails the vertical line test. The vertical line test states that if a vertical line intersects a graph at more than one point, the graph does not represent a function. For a circle, a vertical line can intersect the curve at two points, violating the definition of a function, which requires each input (x-value) to correspond to exactly one output (y-value).

What is completing the square and how is it used in circle equations?

Completing the square is a method used to rewrite quadratic expressions in a perfect square form. For circle equations, it is used to convert the general form to the standard form. To complete the square:

1. Take the middle term (b), divide it by 2, and square the result.
2. Add this squared value to both sides of the equation.
3. Factor the quadratic expression into a binomial square.

This process helps identify the center and radius of the circle for graphing.

How do you find the radius and center of a circle from its equation?

To find the radius and center of a circle from its equation in standard form:

${\left(x,-,h\right)}^2+{\left(y,-,k\right)}^2=r^2$

The center is (h, k), where h and k are the values subtracted from x and y, respectively. The radius is the square root of the constant on the right side of the equation (r²). For example, if the equation is:

${\left(x,-,3\right)}^2+{\left(y,-,4\right)}^2=16$

The center is (3, 4) and the radius is √16 = 4.