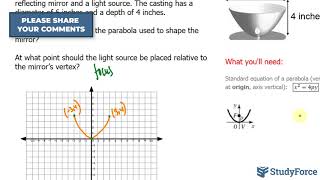
8. Conic Sections
Parabolas
Learn with other creators
Practice this topic
- Multiple Choice
Graph the parabola , and find the focus point and directrix line.
734views - Multiple Choice
If a parabola has the focus at and a directrix line , find the standard equation for the parabola.
607views - Multiple Choice
Graph the parabola , and find the focus point and directrix line.
696views - Multiple Choice
If a parabola has the focus at and a directrix line , find the standard equation for the parabola.
565views1rank - Textbook Question
Find the vertex, focus, and directrix of the parabola with the given equation. Then graph the parabola. x^2 - 4x - 2y = 0
1126views - Textbook Question
Find the standard form of the equation of the parabola satisfying the given conditions. Focus: (12,0); Directrix: x=-12
1326views - Textbook Question
Identify the conic represented by the equation without completing the square. 4x^2 - 9y^2 - 8x + 12y - 144 = 0
1298views - Textbook Question
Find the vertex, focus, and directrix of the parabola with the given equation. Then graph the parabola. (x-4)^2 = 4(y+1)
1218views