Table of contents
- 0. Review of Algebra4h 16m
- 1. Equations & Inequalities3h 18m
- 2. Graphs of Equations43m
- 3. Functions2h 17m
- 4. Polynomial Functions1h 44m
- 5. Rational Functions1h 23m
- 6. Exponential & Logarithmic Functions2h 28m
- 7. Systems of Equations & Matrices4h 6m
- 8. Conic Sections2h 23m
- 9. Sequences, Series, & Induction1h 19m
- 10. Combinatorics & Probability1h 45m
6. Exponential & Logarithmic Functions
The Number e
Problem 48
Textbook Question
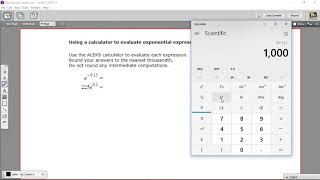
Textbook QuestionGraph each function. Give the domain and range. See Example 3. ƒ(x) = 2^(x+3) +1
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
9mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Exponential Functions
Exponential functions are mathematical expressions in the form f(x) = a * b^(x), where 'a' is a constant, 'b' is the base (a positive real number), and 'x' is the exponent. These functions exhibit rapid growth or decay, depending on the base. In the given function f(x) = 2^(x+3) + 1, the base is 2, indicating that the function will grow exponentially as 'x' increases.
Recommended video:

Exponential Functions
Domain and Range
The domain of a function refers to the set of all possible input values (x-values) for which the function is defined, while the range is the set of all possible output values (f(x)). For the function f(x) = 2^(x+3) + 1, the domain is all real numbers, as there are no restrictions on 'x'. The range, however, is limited to values greater than 1, since the minimum value of 2^(x+3) is 0, making the minimum output 1.
Recommended video:

Domain & Range of Transformed Functions
Graphing Functions
Graphing functions involves plotting points on a coordinate plane to visually represent the relationship between the input (x) and output (f(x)). For exponential functions like f(x) = 2^(x+3) + 1, the graph will show a curve that rises steeply to the right and approaches the horizontal line y = 1 as x decreases. Understanding how to graph these functions helps in visualizing their behavior and identifying key features such as intercepts and asymptotes.
Recommended video:

Graphs of Logarithmic Functions
Related Videos
Related Practice