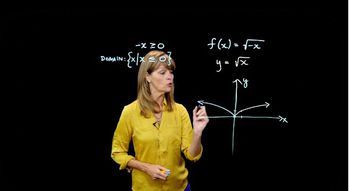Table of contents
- 0. Review of Algebra4h 16m
- 1. Equations & Inequalities3h 18m
- 2. Graphs of Equations43m
- 3. Functions2h 17m
- 4. Polynomial Functions1h 44m
- 5. Rational Functions1h 23m
- 6. Exponential & Logarithmic Functions2h 28m
- 7. Systems of Equations & Matrices4h 6m
- 8. Conic Sections2h 23m
- 9. Sequences, Series, & Induction1h 19m
- 10. Combinatorics & Probability1h 45m
3. Functions
Transformations
Problem 95a
Textbook Question
Textbook QuestionEach of the following graphs is obtained from the graph of ƒ(x)=|x| or g(x)=√x by applying several of the transformations discussed in this section. Describe the transformations and give an equation for the graph. 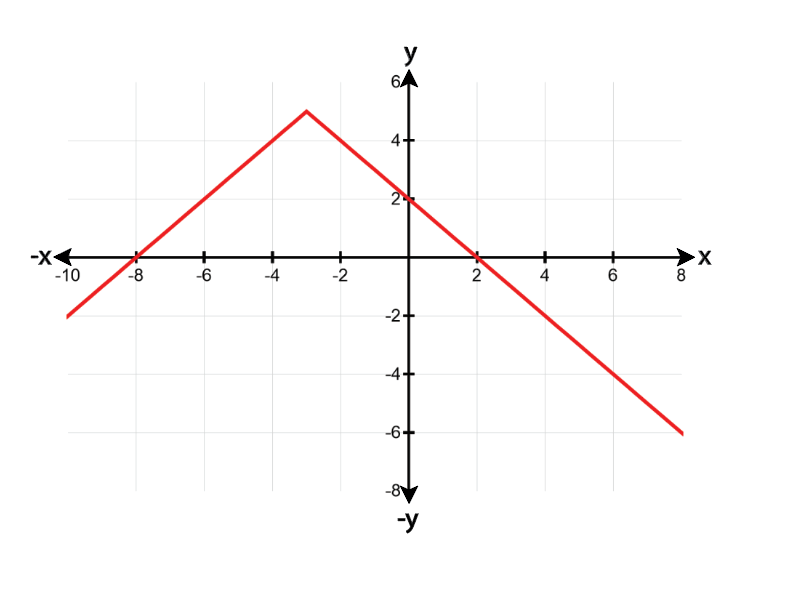
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
2mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Transformations of Functions
Transformations of functions involve altering the graph of a parent function through shifts, stretches, compressions, and reflections. For example, vertical shifts move the graph up or down, while horizontal shifts move it left or right. Understanding these transformations is crucial for describing how the graph of a function changes from its original form.
Recommended video:

Domain & Range of Transformed Functions
Absolute Value Function
The absolute value function, denoted as f(x) = |x|, produces a V-shaped graph that reflects all negative values of x to positive values. This function is essential in understanding how transformations affect its shape and position. When transformed, the peaks and slopes of the graph can change, indicating shifts or reflections.
Recommended video:

Function Composition
Square Root Function
The square root function, represented as g(x) = √x, produces a graph that starts at the origin and increases gradually. This function is important for understanding transformations that may involve vertical or horizontal shifts, as well as reflections. Analyzing how this function behaves under transformations helps in predicting the resulting graph's characteristics.
Recommended video:

Imaginary Roots with the Square Root Property

 5:25m
5:25mWatch next
Master Intro to Transformations with a bite sized video explanation from Nick Kaneko
Start learningRelated Videos
Related Practice