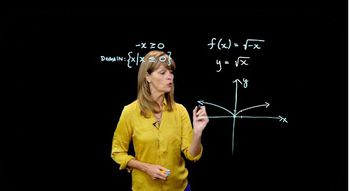Each of the following graphs is obtained from the graph of ƒ(x)=|x| or g(x)=√x by applying several of the transformations discussed in this section. Describe the transformations and give an equation for the graph.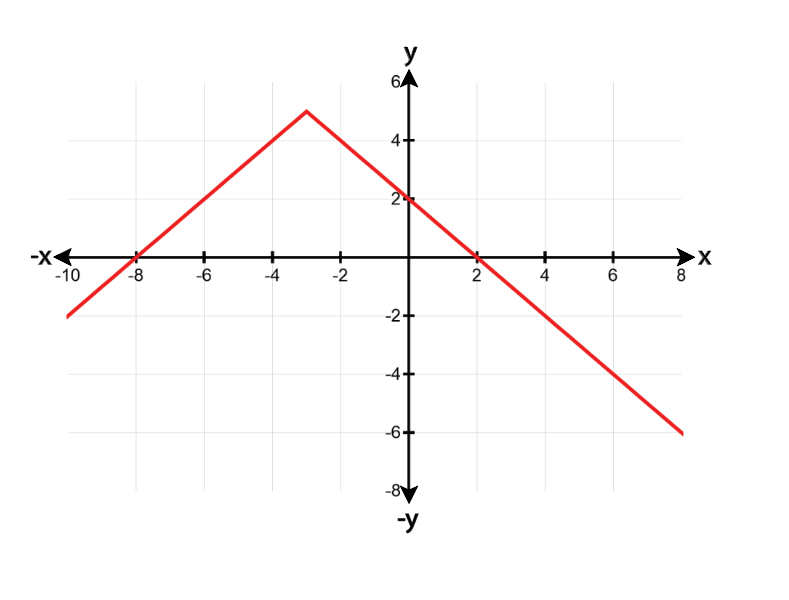

Verified step by step guidance

1. Identify the base function: The base function here is ƒ(x) = |x|, which is a V-shaped graph with its vertex at the origin (0,0).
2. Observe the transformations: The graph appears to be shifted upwards and to the left, and it is also vertically stretched.
3. Determine the vertical shift: The vertex of the graph is at (0, 2), indicating a vertical shift of 2 units upwards.
4. Determine the horizontal shift: The vertex of the graph is at (-3, 2), indicating a horizontal shift of 3 units to the left.
5. Write the transformed equation: Combining these transformations, the equation of the graph is ƒ(x) = 2|x + 3|.

Key Concepts

Transformations of Functions

Transformations of functions involve altering the graph of a parent function through shifts, stretches, compressions, and reflections. For example, vertical shifts move the graph up or down, while horizontal shifts move it left or right. Understanding these transformations is crucial for describing how the graph of a function changes from its original form.

Absolute Value Function

The absolute value function, denoted as f(x) = |x|, produces a V-shaped graph that reflects all negative values of x to positive values. This function is essential in understanding how transformations affect its shape and position. When transformed, the peaks and slopes of the graph can change, indicating shifts or reflections.

Square Root Function

The square root function, represented as g(x) = √x, produces a graph that starts at the origin and increases gradually. This function is important for understanding transformations that may involve vertical or horizontal shifts, as well as reflections. Analyzing how this function behaves under transformations helps in predicting the resulting graph's characteristics.