In Exercises 46–51, evaluate each determinant.

Verified step by step guidance

1. Step 1: Identify the size of the determinant. Determine if it is a 2x2 or 3x3 matrix, as the method to evaluate will differ.
2. Step 2: For a 2x2 matrix, use the formula: \( \text{det}(A) = ad - bc \) where the matrix is \( \begin{bmatrix} a & b \\ c & d \end{bmatrix} \).
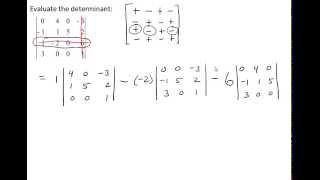
3. Step 3: For a 3x3 matrix, use the rule of Sarrus or the cofactor expansion method. For the rule of Sarrus, extend the first two columns of the matrix to the right and calculate the sum of the products of the diagonals from top left to bottom right, then subtract the sum of the products of the diagonals from bottom left to top right.
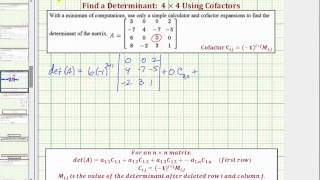
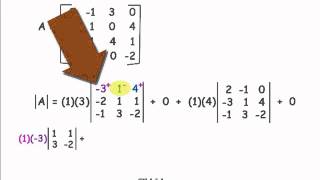
4. Step 4: If using cofactor expansion for a 3x3 matrix, choose a row or column to expand along. Calculate the determinant by summing the products of each element in the row or column with its corresponding cofactor.
5. Step 5: Simplify the expression obtained from the previous steps to find the determinant value.

Key Concepts

Determinants

A determinant is a scalar value that can be computed from the elements of a square matrix. It provides important information about the matrix, such as whether it is invertible (non-zero determinant) or singular (zero determinant). Determinants can be calculated using various methods, including expansion by minors or row reduction.

Square Matrices

A square matrix is a matrix with the same number of rows and columns, denoted as n x n. Determinants are only defined for square matrices, as they represent linear transformations in n-dimensional space. Understanding the structure of square matrices is essential for evaluating their determinants.

Properties of Determinants

Determinants have several key properties that simplify their computation and understanding. For example, the determinant of a product of matrices equals the product of their determinants, and swapping two rows of a matrix changes the sign of the determinant. Familiarity with these properties can help in efficiently evaluating determinants.