Table of contents
- 0. Review of Algebra4h 16m
- 1. Equations & Inequalities3h 18m
- 2. Graphs of Equations43m
- 3. Functions2h 17m
- 4. Polynomial Functions1h 44m
- 5. Rational Functions1h 23m
- 6. Exponential & Logarithmic Functions2h 28m
- 7. Systems of Equations & Matrices4h 6m
- 8. Conic Sections2h 23m
- 9. Sequences, Series, & Induction1h 19m
- 10. Combinatorics & Probability1h 45m
7. Systems of Equations & Matrices
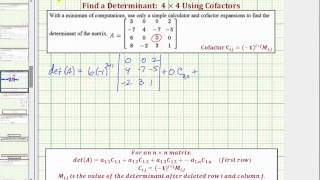
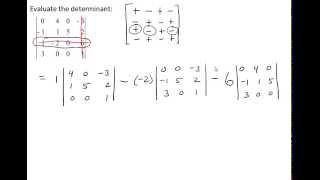
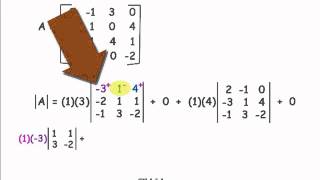
Determinants and Cramer's Rule
Problem 37e
Textbook Question
In Exercises 37–38, find the products and to determine whether B is the multiplicative inverse of A.
 Verified step by step guidance
Verified step by step guidance1
<Step 1: Understand the concept of multiplicative inverse. The multiplicative inverse of a matrix A is another matrix B such that when A is multiplied by B, the result is the identity matrix.>
<Step 2: Identify matrices A and B from the problem statement.>
<Step 3: Multiply matrix A by matrix B. Use the matrix multiplication rules: the element in the ith row and jth column of the product is the sum of the products of the elements of the ith row of the first matrix and the jth column of the second matrix.>
<Step 4: Check if the resulting product is the identity matrix. The identity matrix has 1s on the diagonal and 0s elsewhere.>
<Step 5: Conclude whether B is the multiplicative inverse of A based on whether the product is the identity matrix.>
Recommended similar problem, with video answer:
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
12mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Matrix Multiplication
Matrix multiplication involves combining two matrices to produce a third matrix. The number of columns in the first matrix must equal the number of rows in the second matrix. The resulting matrix's elements are calculated by taking the dot product of the rows of the first matrix with the columns of the second matrix. Understanding this operation is crucial for determining the product of matrices A and B.
Recommended video:

Finding Zeros & Their Multiplicity
Multiplicative Inverse
The multiplicative inverse of a matrix A is another matrix, denoted as A⁻¹, such that when A is multiplied by A⁻¹, the result is the identity matrix I. The identity matrix acts like the number 1 in regular multiplication, meaning that A * A⁻¹ = I. To determine if B is the multiplicative inverse of A, one must verify if the product AB equals the identity matrix.
Recommended video:

Finding Zeros & Their Multiplicity
Identity Matrix
An identity matrix is a square matrix with ones on the diagonal and zeros elsewhere. It serves as the multiplicative identity in matrix algebra, meaning that any matrix multiplied by the identity matrix remains unchanged. For a matrix A of size n x n, the identity matrix I will also be of size n x n, and confirming that the product of A and its supposed inverse B yields I is essential for validating B as A's inverse.
Recommended video:
Guided course

Introduction to Matrices

 4:36m
4:36mWatch next
Master Determinants of 2×2 Matrices with a bite sized video explanation from Patrick Ford
Start learningRelated Videos
Related Practice