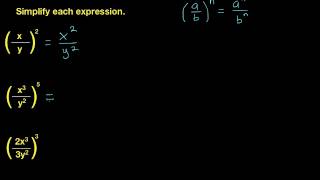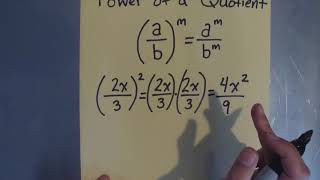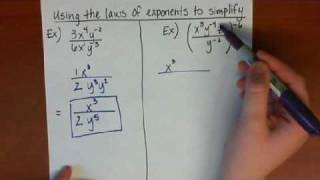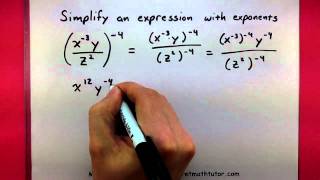A football was kicked vertically upward from a height of 4 feet with an initial speed of 60 feet per second. The formula h=4+60t-16t^2 describes the ball's height above the ground, h, in feet, t seconds after it was kicked. Use this formula to solve Exercises 19–20. What was the ball's height 2 seconds after it was kicked?

Key Concepts

Quadratic Functions

A quadratic function is a polynomial function of degree two, typically expressed in the form f(t) = at^2 + bt + c. In this context, the height of the football is modeled by a quadratic equation, where the term -16t^2 represents the effect of gravity on the ball's height over time. Understanding the properties of quadratic functions, such as their parabolas and vertex, is essential for analyzing the motion of the ball.

Substitution

Substitution is a mathematical technique used to replace a variable with a specific value to evaluate an expression or function. In this problem, we substitute t = 2 seconds into the height formula h = 4 + 60t - 16t^2 to find the ball's height at that specific time. Mastering substitution is crucial for solving equations and understanding how changes in variables affect outcomes.

Projectile Motion

Projectile motion refers to the motion of an object that is thrown or projected into the air, influenced by gravity. The height formula provided captures the essence of projectile motion, where the initial height and speed determine the trajectory of the ball. Recognizing the principles of projectile motion helps in predicting the behavior of objects in free fall and understanding the effects of gravitational acceleration.