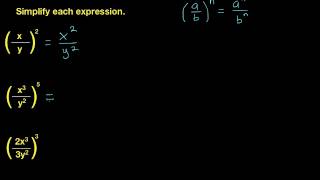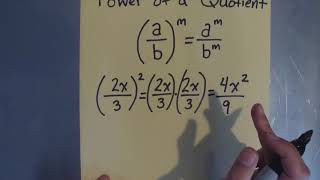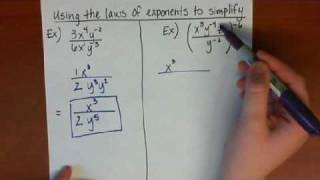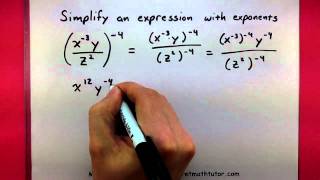Table of contents
- 0. Review of Algebra4h 16m
- 1. Equations & Inequalities3h 18m
- 2. Graphs of Equations43m
- 3. Functions2h 17m
- 4. Polynomial Functions1h 44m
- 5. Rational Functions1h 23m
- 6. Exponential & Logarithmic Functions2h 28m
- 7. Systems of Equations & Matrices4h 6m
- 8. Conic Sections2h 23m
- 9. Sequences, Series, & Induction1h 19m
- 10. Combinatorics & Probability1h 45m
0. Review of Algebra
Exponents
Problem 36b
Textbook Question
Textbook QuestionInsert ∈ or ∉ in each blank to make the resulting statement true. {2} ____ {2, 4, 6, 8}
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
1mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Set Notation
Set notation is a mathematical language used to describe collections of objects, known as sets. In this context, the set {2, 4, 6, 8} contains the elements 2, 4, 6, and 8. Understanding how to read and interpret set notation is essential for determining relationships between individual elements and sets.
Recommended video:

Interval Notation
Element of a Set
The concept of an element of a set refers to whether a specific item belongs to a given set. The symbol '∈' indicates that an element is a member of a set, while '∉' indicates that it is not. For example, since 2 is included in the set {2, 4, 6, 8}, the correct symbol to use in this case would be '∈'.
Recommended video:

Graphing Polynomial Functions
Logical Statements
Logical statements are assertions that can be evaluated as true or false. In this question, the task is to determine the truth value of the statement involving the element 2 and the set {2, 4, 6, 8}. Understanding how to construct and evaluate these statements is crucial for correctly filling in the blanks with the appropriate symbols.
Recommended video:
Guided course

Classifying Systems of Linear Equations

 7:39m
7:39mWatch next
Master Introduction to Exponent Rules with a bite sized video explanation from Patrick Ford
Start learningRelated Videos
Related Practice