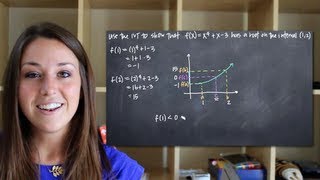Use the intermediate value theorem to show that each polynomial function has a real zero between the numbers given. See Example 5. ƒ(x)=-2x^3+5x^2+5x-7; 0 and 1

Key Concepts

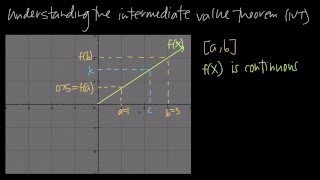
Intermediate Value Theorem

The Intermediate Value Theorem states that if a continuous function takes on two values at two points, then it must take on every value between those two points at least once. This theorem is crucial for proving the existence of roots in polynomial functions, as it guarantees that if the function changes sign over an interval, there is at least one real zero within that interval.

Polynomial Functions

Polynomial functions are mathematical expressions involving variables raised to whole number powers, combined using addition, subtraction, and multiplication. They are continuous and smooth, which means they do not have breaks or sharp corners. Understanding the behavior of polynomial functions, such as their end behavior and turning points, is essential for applying the Intermediate Value Theorem effectively.

Sign Change

A sign change occurs when a function's value transitions from positive to negative or vice versa. In the context of the Intermediate Value Theorem, identifying a sign change between two points indicates that there is at least one real zero in that interval. For the polynomial function given, evaluating the function at the endpoints (0 and 1) will help determine if a sign change exists, confirming the presence of a root.