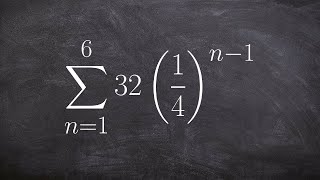Table of contents
- 0. Review of Algebra4h 16m
- 1. Equations & Inequalities3h 18m
- 2. Graphs of Equations43m
- 3. Functions2h 17m
- 4. Polynomial Functions1h 44m
- 5. Rational Functions1h 23m
- 6. Exponential & Logarithmic Functions2h 28m
- 7. Systems of Equations & Matrices4h 6m
- 8. Conic Sections2h 23m
- 9. Sequences, Series, & Induction1h 19m
- 10. Combinatorics & Probability1h 45m
9. Sequences, Series, & Induction
Geometric Sequences
Problem 27
Textbook Question
Textbook QuestionUse the formula for the sum of the first n terms of a geometric sequence to solve Exercises 25–30. Find the sum of the first 11 terms of the geometric sequence: 3, - 6, 12, - 24, ...
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
4mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Geometric Sequence
A geometric sequence is a sequence of numbers where each term after the first is found by multiplying the previous term by a fixed, non-zero number called the common ratio. In the given sequence, the first term is 3, and the common ratio can be determined by dividing any term by its preceding term, which in this case is -2.
Recommended video:
Guided course

Geometric Sequences - Recursive Formula
Sum of the First n Terms
The sum of the first n terms of a geometric sequence can be calculated using the formula S_n = a(1 - r^n) / (1 - r), where S_n is the sum, a is the first term, r is the common ratio, and n is the number of terms. This formula is applicable when the common ratio r is not equal to 1, allowing for efficient calculation of the sum without needing to add each term individually.
Recommended video:
Guided course

Example 1
Common Ratio
The common ratio in a geometric sequence is the factor by which we multiply each term to get the next term. It is crucial for determining the behavior of the sequence and calculating the sum of its terms. In the provided sequence, the common ratio is -2, which indicates that the terms alternate in sign and increase in absolute value.
Recommended video:

Graphs of Common Functions

 4:18m
4:18mWatch next
Master Geometric Sequences - Recursive Formula with a bite sized video explanation from Patrick Ford
Start learningRelated Videos
Related Practice