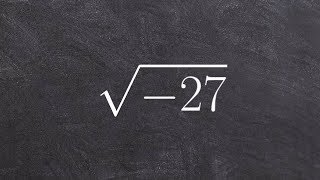In Exercises 53–60, write each power of i as as i, - 1, - i, or 1. i^31

Verified step by step guidance

1. Recognize that the powers of \(i\) cycle every four: \(i^1 = i\), \(i^2 = -1\), \(i^3 = -i\), \(i^4 = 1\).
2. To find \(i^{31}\), determine the remainder when 31 is divided by 4, since the powers of \(i\) repeat every 4.
3. Calculate \(31 \div 4\) to find the quotient and remainder.
4. The remainder of \(31 \div 4\) is 3, which corresponds to \(i^3\) in the cycle.
5. Therefore, \(i^{31} = i^3 = -i\).

Key Concepts

Powers of i

The imaginary unit i is defined as the square root of -1. The powers of i cycle through four distinct values: i^1 = i, i^2 = -1, i^3 = -i, and i^4 = 1. This cyclical pattern repeats every four powers, which is essential for simplifying higher powers of i.

Modulus and Division

To simplify powers of i, we can use the modulus of the exponent with respect to 4. For example, to find i^31, we calculate 31 mod 4, which gives us a remainder of 3. This means i^31 is equivalent to i^3, allowing us to simplify the expression effectively.

Complex Numbers

Complex numbers are numbers that have a real part and an imaginary part, expressed in the form a + bi, where a and b are real numbers. Understanding complex numbers is crucial when working with powers of i, as it provides context for their applications in mathematics and engineering.