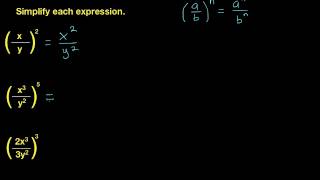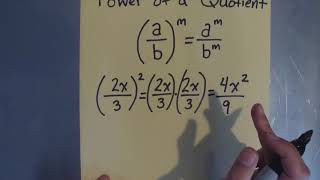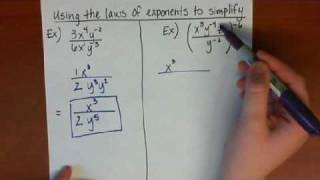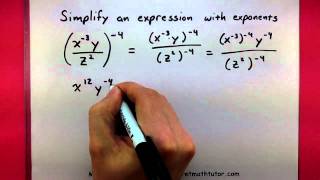Let U = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13}, M = {0, 2, 4, 6, 8}, N = {1, 3, 5, 7, 9, 11, 13}, Q = {0, 2, 4, 6, 8, 10, 12}, and R = {0, 1, 2, 3, 4}.Use these sets to find each of the following. Identify any disjoint sets. {x | x ∈ M or x ∈ Q}

Key Concepts

Sets and Set Notation

A set is a collection of distinct objects, considered as an object in its own right. Set notation uses curly braces to define a set, with elements separated by commas. Understanding how to read and write sets is crucial for manipulating them, such as identifying unions, intersections, and differences between sets.

Union of Sets

The union of two sets combines all unique elements from both sets. It is denoted by the symbol '∪'. For example, if M = {0, 2, 4, 6, 8} and Q = {0, 2, 4, 6, 8, 10, 12}, the union M ∪ Q includes all elements from both sets without duplication, resulting in {0, 2, 4, 6, 8, 10, 12}.

Disjoint Sets

Disjoint sets are sets that have no elements in common, meaning their intersection is the empty set. For instance, if M = {0, 2, 4, 6, 8} and N = {1, 3, 5, 7, 9, 11, 13}, these sets are disjoint because they do not share any elements. Identifying disjoint sets is important for understanding relationships between different collections of objects.