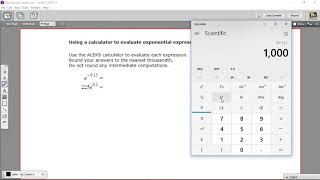
In Exercises 1–10, approximate each number using a calculator. Round your answer to three decimal places. e^-0.95

Key Concepts

Exponential Functions

Exponential functions are mathematical expressions in the form of f(x) = a * b^x, where 'a' is a constant, 'b' is the base, and 'x' is the exponent. In this case, e^-0.95 represents an exponential function where the base 'e' (approximately 2.718) is raised to a negative exponent. Understanding how to evaluate exponential functions is crucial for solving problems involving growth or decay.

The Number 'e'

The number 'e' is a mathematical constant approximately equal to 2.71828, and it serves as the base for natural logarithms. It is significant in calculus and complex analysis, particularly in modeling continuous growth or decay processes. Recognizing 'e' and its properties is essential for accurately calculating expressions involving exponential functions.

Rounding Numbers

Rounding numbers involves adjusting a number to a specified degree of accuracy, often to simplify calculations or present results clearly. In this context, rounding to three decimal places means keeping three digits after the decimal point and adjusting the last digit based on the value of the next digit. Mastery of rounding techniques is important for ensuring precision in mathematical results.