Table of contents
- 0. Review of Algebra4h 16m
- 1. Equations & Inequalities3h 18m
- 2. Graphs of Equations43m
- 3. Functions2h 17m
- 4. Polynomial Functions1h 44m
- 5. Rational Functions1h 23m
- 6. Exponential & Logarithmic Functions2h 28m
- 7. Systems of Equations & Matrices4h 6m
- 8. Conic Sections2h 23m
- 9. Sequences, Series, & Induction1h 19m
- 10. Combinatorics & Probability1h 45m
0. Review of Algebra
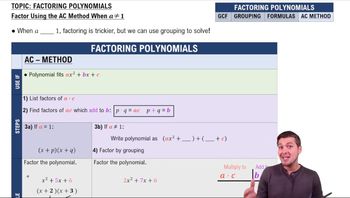
Factoring Polynomials
Problem 53b
Textbook Question
Factor each trinomial, if possible. See Examples 3 and 4. 32a^2+48ab+18b^2
 Verified step by step guidance
Verified step by step guidance1
Identify the greatest common factor (GCF) of the coefficients in the trinomial: 32, 48, and 18.
Factor out the GCF from the trinomial. In this case, the GCF is 2.
Rewrite the trinomial as 2(16a^2 + 24ab + 9b^2).
Look for two numbers that multiply to the product of the first and last coefficients (16 * 9) and add to the middle coefficient (24).
Use these numbers to factor the quadratic expression inside the parentheses into two binomials.
 Verified video answer for a similar problem:
Verified video answer for a similar problem:This video solution was recommended by our tutors as helpful for the problem above
Video duration:
4mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Factoring Trinomials
Factoring trinomials involves rewriting a quadratic expression in the form ax^2 + bx + c as a product of two binomials. This process often requires identifying two numbers that multiply to ac (the product of the coefficient of x^2 and the constant term) and add to b (the coefficient of x). Understanding this concept is crucial for simplifying expressions and solving equations.
Recommended video:
Guided course

Factor Using Special Product Formulas
Greatest Common Factor (GCF)
The greatest common factor (GCF) is the largest factor that divides all terms in a polynomial. Before factoring a trinomial, it is often beneficial to factor out the GCF, as it simplifies the expression and makes the subsequent factoring process easier. Identifying the GCF is a fundamental skill in polynomial manipulation.
Recommended video:

Graphs of Common Functions
Quadratic Formula
The quadratic formula, given by x = (-b ± √(b² - 4ac)) / (2a), provides a method for finding the roots of a quadratic equation. While not directly used for factoring, it helps in understanding the relationship between the coefficients of a trinomial and its roots. This knowledge can assist in verifying the correctness of the factored form.
Recommended video:

Solving Quadratic Equations Using The Quadratic Formula

 7:30m
7:30mWatch next
Master Introduction to Factoring Polynomials with a bite sized video explanation from Patrick Ford
Start learningRelated Videos
Related Practice