Table of contents
- 0. Review of Algebra4h 16m
- 1. Equations & Inequalities3h 18m
- 2. Graphs of Equations43m
- 3. Functions2h 17m
- 4. Polynomial Functions1h 44m
- 5. Rational Functions1h 23m
- 6. Exponential & Logarithmic Functions2h 28m
- 7. Systems of Equations & Matrices4h 6m
- 8. Conic Sections2h 23m
- 9. Sequences, Series, & Induction1h 19m
- 10. Combinatorics & Probability1h 45m
3. Functions
Intro to Functions & Their Graphs
Problem 77b
Textbook Question
Textbook QuestionIn Exercises 76–81, find the domain of each function. g(x) = 4/(x - 7)
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
1mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Domain of a Function
The domain of a function refers to the set of all possible input values (x-values) for which the function is defined. For rational functions, the domain is typically restricted by values that would make the denominator zero, as division by zero is undefined.
Recommended video:

Domain Restrictions of Composed Functions
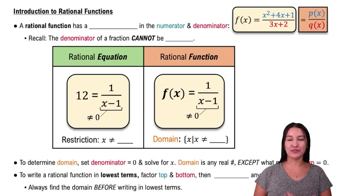
Rational Functions
A rational function is a function that can be expressed as the ratio of two polynomials. In the case of g(x) = 4/(x - 7), the numerator is a constant (4) and the denominator is a linear polynomial (x - 7). Understanding the structure of rational functions is essential for determining their domains.
Recommended video:
Intro to Rational Functions
Finding Restrictions
To find the domain of a function, one must identify any restrictions on the input values. For g(x) = 4/(x - 7), the restriction arises from the denominator, which cannot equal zero. Thus, solving the equation x - 7 = 0 reveals that x cannot be 7, leading to the conclusion that the domain excludes this value.
Recommended video:

Restrictions on Rational Equations

 5:2m
5:2mWatch next
Master Relations and Functions with a bite sized video explanation from Nick Kaneko
Start learningRelated Videos
Related Practice






