Table of contents
- 0. Review of Algebra4h 16m
- 1. Equations & Inequalities3h 18m
- 2. Graphs of Equations43m
- 3. Functions2h 17m
- 4. Polynomial Functions1h 44m
- 5. Rational Functions1h 23m
- 6. Exponential & Logarithmic Functions2h 28m
- 7. Systems of Equations & Matrices4h 6m
- 8. Conic Sections2h 23m
- 9. Sequences, Series, & Induction1h 19m
- 10. Combinatorics & Probability1h 45m
2. Graphs of Equations
Lines
Problem 60
Textbook Question
In Exercises 59-66, a. Rewrite the given equation in slope-intercept form. b. Give the slope and y-intercept. c. Use the slope and y-intercept to graph the linear function. 4x+y-6=0
 Verified step by step guidance
Verified step by step guidance1
**Step 1:** Start with the given equation: \(4x + y - 6 = 0\).
**Step 2:** To rewrite the equation in slope-intercept form \(y = mx + b\), solve for \(y\). Begin by isolating \(y\) on one side of the equation. Subtract \(4x\) from both sides: \(y - 6 = -4x\).
**Step 3:** Add \(6\) to both sides to solve for \(y\): \(y = -4x + 6\). Now, the equation is in slope-intercept form \(y = mx + b\), where \(m\) is the slope and \(b\) is the y-intercept.
**Step 4:** Identify the slope \(m\) and y-intercept \(b\) from the equation \(y = -4x + 6\). The slope \(m\) is \(-4\) and the y-intercept \(b\) is \(6\).
**Step 5:** To graph the linear function, start by plotting the y-intercept \((0, 6)\) on the graph. Then, use the slope \(-4\), which means \(-4/1\), to find another point. From \((0, 6)\), move down 4 units and right 1 unit to plot the next point. Draw a line through these points to complete the graph.
Recommended similar problem, with video answer:
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
5mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Slope-Intercept Form
The slope-intercept form of a linear equation is expressed as y = mx + b, where m represents the slope and b represents the y-intercept. This form is particularly useful for quickly identifying the slope and y-intercept of a line, which are essential for graphing linear functions.
Recommended video:
Guided course
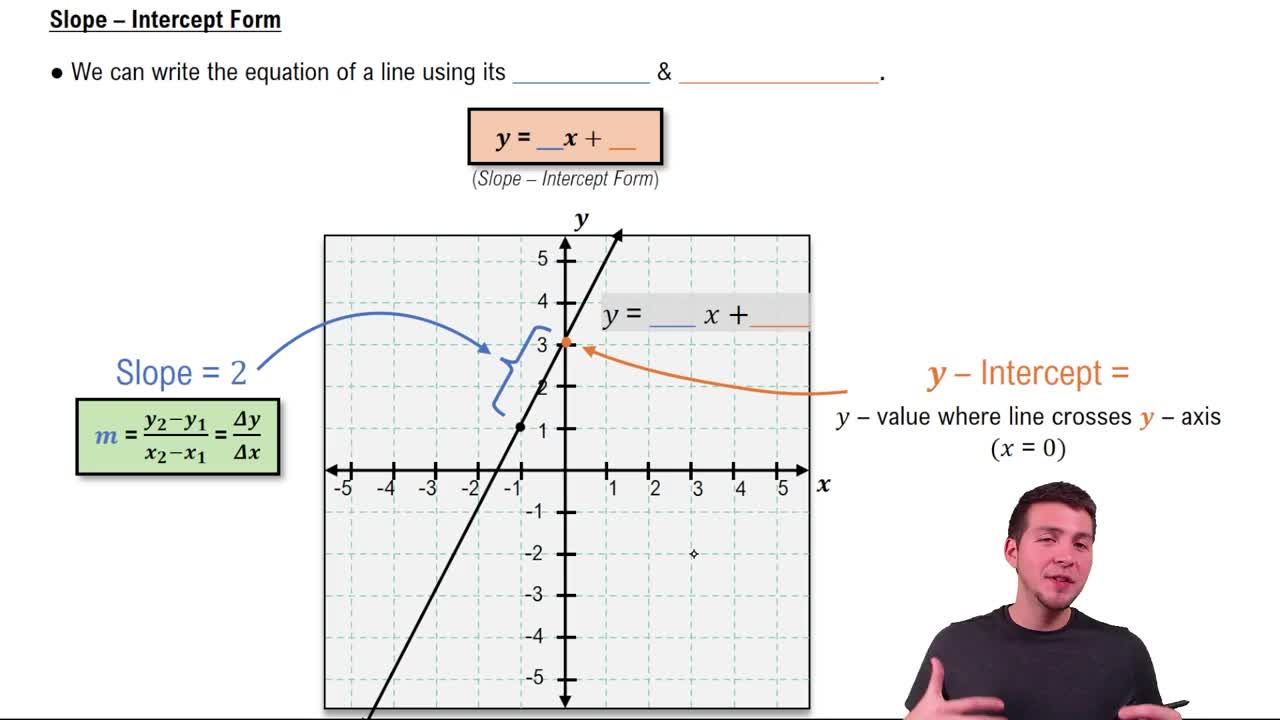
Slope-Intercept Form
Slope
The slope of a line measures its steepness and direction, calculated as the change in y over the change in x (rise over run). A positive slope indicates the line rises from left to right, while a negative slope indicates it falls. Understanding slope is crucial for interpreting the relationship between variables in a linear equation.
Recommended video:
Guided course

Types of Slope
Y-Intercept
The y-intercept is the point where a line crosses the y-axis, represented by the value of y when x is zero. In the slope-intercept form, this value is denoted by b. Knowing the y-intercept is important for graphing linear equations, as it provides a starting point on the graph.
Recommended video:
Guided course

Graphing Intercepts

 6:49m
6:49mWatch next
Master The Slope of a Line with a bite sized video explanation from Patrick Ford
Start learningRelated Videos
Related Practice










