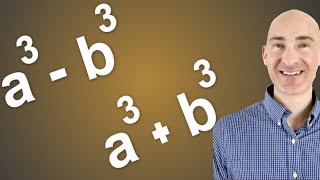Table of contents
- 0. Review of Algebra4h 16m
- 1. Equations & Inequalities3h 18m
- 2. Graphs of Equations43m
- 3. Functions2h 17m
- 4. Polynomial Functions1h 44m
- 5. Rational Functions1h 23m
- 6. Exponential & Logarithmic Functions2h 28m
- 7. Systems of Equations & Matrices4h 6m
- 8. Conic Sections2h 23m
- 9. Sequences, Series, & Induction1h 19m
- 10. Combinatorics & Probability1h 45m
0. Review of Algebra
Factoring Polynomials
Problem 48b
Textbook Question
Multiply or divide, as indicated. ac + ad + bc + bd/a^2 - b^2 * a^3 - b^3/2a^2 + 2ab + 2b^2
 Verified step by step guidance
Verified step by step guidance1
Factor the numerator of the first fraction: \( ac + ad + bc + bd \). Notice that it can be grouped as \((ac + ad) + (bc + bd)\), which can be factored further as \(a(c + d) + b(c + d) = (a + b)(c + d)\).
Factor the denominator of the first fraction: \(a^2 - b^2\). This is a difference of squares, which can be factored as \((a - b)(a + b)\).
Factor the numerator of the second fraction: \(a^3 - b^3\). This is a difference of cubes, which can be factored as \((a - b)(a^2 + ab + b^2)\).
Factor the denominator of the second fraction: \(2a^2 + 2ab + 2b^2\). Notice that 2 is a common factor, so factor it out to get \(2(a^2 + ab + b^2)\).
Combine the fractions by multiplying them: \(\frac{(a + b)(c + d)}{(a - b)(a + b)} \times \frac{(a - b)(a^2 + ab + b^2)}{2(a^2 + ab + b^2)}\). Cancel out the common factors in the numerator and the denominator.
Recommended similar problem, with video answer:
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
8mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
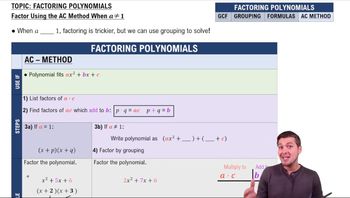
Factoring Polynomials
Factoring polynomials involves rewriting a polynomial as a product of its factors. This is essential for simplifying expressions, especially when dealing with terms like ac + ad + bc + bd. Recognizing common factors or using techniques such as grouping can help in breaking down complex expressions into simpler components.
Recommended video:
Guided course

Introduction to Factoring Polynomials
Rational Expressions
Rational expressions are fractions where the numerator and/or denominator are polynomials. Understanding how to manipulate these expressions, including multiplying and dividing them, is crucial for solving problems involving algebraic fractions. This includes knowing how to find a common denominator and simplifying the resulting expression.
Recommended video:
Guided course

Rationalizing Denominators
Algebraic Identities
Algebraic identities are equations that hold true for all values of the variables involved. Familiarity with identities such as the difference of squares (a^2 - b^2) and the sum/difference of cubes (a^3 ± b^3) is important for simplifying expressions. These identities can often be used to transform complex expressions into more manageable forms.
Recommended video:
Guided course

Introduction to Algebraic Expressions

 7:30m
7:30mWatch next
Master Introduction to Factoring Polynomials with a bite sized video explanation from Patrick Ford
Start learningRelated Videos
Related Practice