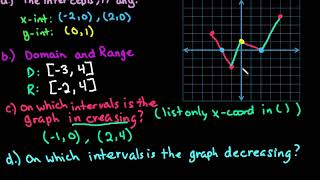Table of contents
- 0. Review of Algebra4h 16m
- 1. Equations & Inequalities3h 18m
- 2. Graphs of Equations43m
- 3. Functions2h 17m
- 4. Polynomial Functions1h 44m
- 5. Rational Functions1h 23m
- 6. Exponential & Logarithmic Functions2h 28m
- 7. Systems of Equations & Matrices4h 6m
- 8. Conic Sections2h 23m
- 9. Sequences, Series, & Induction1h 19m
- 10. Combinatorics & Probability1h 45m
2. Graphs of Equations
Graphs and Coordinates
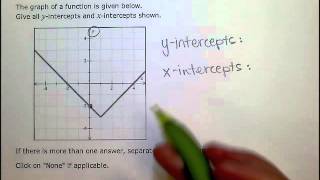
Problem 86
Textbook Question
Textbook QuestionIn Exercises 85–90, find the x-intercepts of the graph of each equation. Then use the x-intercepts to match the equation with its graph. [The graphs are labeled (a) through (f).] y = √(x - 4) + √(x + 4) - 4
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
1mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
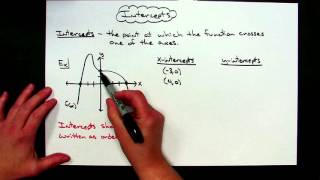
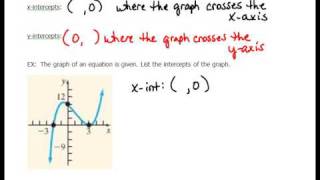
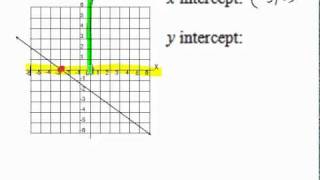
X-Intercepts
X-intercepts are the points where a graph intersects the x-axis, which occurs when the value of y is zero. To find the x-intercepts of an equation, you set y equal to zero and solve for x. This is crucial for understanding the behavior of the graph and identifying key points that help in graphing the function.
Recommended video:
Guided course

Graphing Intercepts
Square Root Functions
Square root functions, such as y = √(x - a), are defined for values of x that make the expression under the square root non-negative. This means that the domain of the function is limited to x values greater than or equal to a. Understanding the domain is essential for determining where the function is valid and for finding x-intercepts.
Recommended video:

Imaginary Roots with the Square Root Property
Graph Matching
Graph matching involves comparing the characteristics of a function's graph with given options to identify the correct representation. This requires understanding the shape and key features of the graph, such as intercepts, asymptotes, and overall behavior. By analyzing the x-intercepts and other properties, one can effectively match the equation to its corresponding graph.
Recommended video:

Graphing Logarithmic Functions

 5:10m
5:10mWatch next
Master Graphs & the Rectangular Coordinate System with a bite sized video explanation from Patrick Ford
Start learningRelated Videos
Related Practice