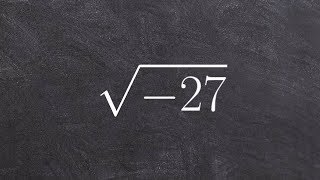Find each sum or difference. Write answers in standard form. (-3+2i) - (-4+2i)

Key Concepts

Complex Numbers

Complex numbers are numbers that have a real part and an imaginary part, expressed in the form a + bi, where 'a' is the real part and 'b' is the coefficient of the imaginary unit 'i', which is defined as the square root of -1. Understanding complex numbers is essential for performing operations such as addition and subtraction.

Addition and Subtraction of Complex Numbers

To add or subtract complex numbers, you combine their real parts and their imaginary parts separately. For example, when adding (a + bi) and (c + di), the result is (a + c) + (b + d)i. This concept is crucial for solving problems involving complex numbers, as it allows for straightforward calculations.

Standard Form of Complex Numbers

The standard form of a complex number is expressed as a + bi, where 'a' and 'b' are real numbers. Writing complex numbers in standard form is important for clarity and consistency, especially when performing operations or comparing different complex numbers.