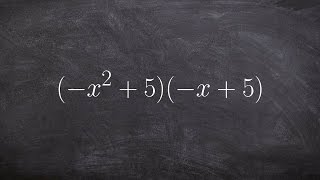In Exercises 83–94, find each product. (x + y + 3)(x + y − 3)

Key Concepts

Polynomial Multiplication

Polynomial multiplication involves distributing each term in one polynomial to every term in another polynomial. This process is often referred to as the FOIL method for binomials, which stands for First, Outside, Inside, Last. In the given expression, each term in the first polynomial must be multiplied by each term in the second polynomial to find the complete product.

Difference of Squares

The difference of squares is a specific algebraic identity that states that the product of two binomials in the form (a + b)(a - b) equals a² - b². This identity simplifies the multiplication process significantly. In the given expression, recognizing that (x + y + 3)(x + y - 3) can be treated as a difference of squares can lead to a quicker solution.

Combining Like Terms

Combining like terms is the process of simplifying an expression by adding or subtracting terms that have the same variable raised to the same power. After multiplying polynomials, the resulting expression may contain several like terms that can be combined to produce a more concise form. This step is crucial for presenting the final answer in its simplest form.