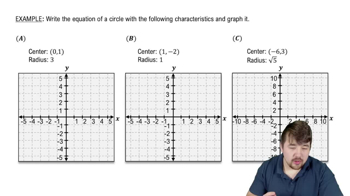
Identify and sketch the graph of each relation.
$3x^2+6x+3y^2-12y=12$

Verified step by step guidance

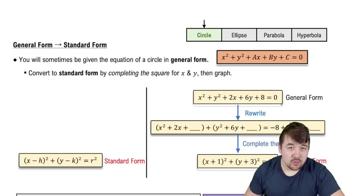
1. Start by rewriting the given equation: \(3x^2 + 6x + 3y^2 - 12y = 12\). Notice that each term involving \(x\) and \(y\) can be grouped together.
2. Factor out the common factor of 3 from each term: \(3(x^2 + 2x) + 3(y^2 - 4y) = 12\).
3. Divide the entire equation by 3 to simplify: \(x^2 + 2x + y^2 - 4y = 4\).
4. Complete the square for the \(x\) terms: \(x^2 + 2x\). Add and subtract \(1\) (\((\frac{2}{2})^2\)) to complete the square: \((x + 1)^2 - 1\).
5. Complete the square for the \(y\) terms: \(y^2 - 4y\). Add and subtract \(4\) (\((\frac{-4}{2})^2\)) to complete the square: \((y - 2)^2 - 4\).