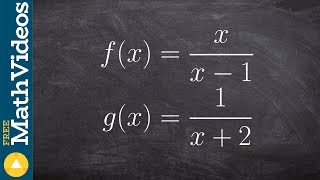For the pair of functions defined, find (f/g)(x).Give the domain of each. See Example 2. ƒ(x)=√(4x-1), g(x)=1/x

Verified step by step guidance

1. Step 1: Determine the expression for the function (f/g)(x). This is done by dividing the function f(x) by g(x). So, (f/g)(x) = f(x) / g(x) = \sqrt{4x-1} / \frac{1}{x}.
2. Step 2: Simplify the expression for (f/g)(x). Multiply the numerator by the reciprocal of the denominator: (f/g)(x) = \sqrt{4x-1} \cdot x.
3. Step 3: Identify the domain of f(x) = \sqrt{4x-1}. The expression under the square root must be non-negative, so set up the inequality 4x - 1 \geq 0 and solve for x.
4. Step 4: Identify the domain of g(x) = 1/x. The denominator cannot be zero, so x cannot be equal to 0.
5. Step 5: Combine the domains from steps 3 and 4 to find the domain of (f/g)(x). The domain of (f/g)(x) is all x values that satisfy both conditions: x must be greater than or equal to 1/4 and x cannot be 0.

Key Concepts

Function Division

Function division involves creating a new function by dividing one function by another. In this case, (f/g)(x) is defined as f(x) divided by g(x), which requires both functions to be defined at the same x-value. Understanding how to perform this operation is crucial for finding the resulting function.

Domain of a Function

The domain of a function is the set of all possible input values (x-values) for which the function is defined. For the functions given, the domain must consider restrictions such as square roots (which require non-negative inputs) and denominators (which cannot be zero). Identifying the domain is essential for ensuring the function behaves correctly.

Square Root Function

A square root function, like f(x) = √(4x - 1), is defined only for values of x that make the expression under the square root non-negative. This means that 4x - 1 must be greater than or equal to zero, leading to a specific range of x-values. Understanding this concept is vital for determining the domain of f(x).