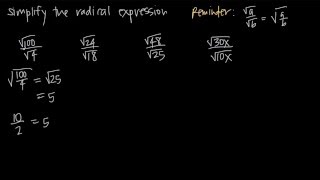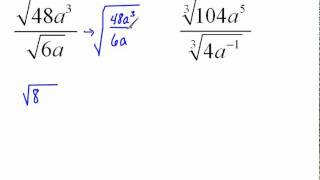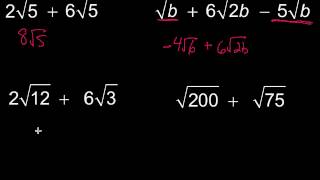Table of contents
- 0. Review of Algebra4h 16m
- 1. Equations & Inequalities3h 18m
- 2. Graphs of Equations43m
- 3. Functions2h 17m
- 4. Polynomial Functions1h 44m
- 5. Rational Functions1h 23m
- 6. Exponential & Logarithmic Functions2h 28m
- 7. Systems of Equations & Matrices4h 6m
- 8. Conic Sections2h 23m
- 9. Sequences, Series, & Induction1h 19m
- 10. Combinatorics & Probability1h 45m
0. Review of Algebra
Radical Expressions
Problem 85b
Textbook Question
Simplify each radical. Assume all variables represent positive real numbers. ∜(x⁴ + y⁴)
 Verified step by step guidance
Verified step by step guidance1
Identify the expression inside the radical: \(x^4 + y^4\).
Recognize that the expression is under a fourth root, denoted as \(\sqrt[4]{x^4 + y^4}\).
Since \(x^4\) and \(y^4\) are both perfect fourth powers, consider simplifying each term separately if possible.
Note that \(\sqrt[4]{x^4} = x\) and \(\sqrt[4]{y^4} = y\), but the expression \(x^4 + y^4\) does not allow for direct simplification into a single term.
Conclude that \(\sqrt[4]{x^4 + y^4}\) cannot be simplified further without additional context or constraints.
Recommended similar problem, with video answer:
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
1mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Radical Expressions
Radical expressions involve roots, such as square roots, cube roots, and higher-order roots. In this context, the expression ∜(x⁴ + y⁴) represents the fourth root of the sum of x raised to the fourth power and y raised to the fourth power. Understanding how to manipulate and simplify these expressions is crucial for solving problems involving radicals.
Recommended video:
Guided course

Radical Expressions with Fractions
Properties of Exponents
The properties of exponents govern how to simplify expressions involving powers. For instance, x⁴ can be expressed as (x²)², which helps in simplifying radical expressions. Recognizing these properties allows for the effective reduction of complex expressions into simpler forms, particularly when dealing with roots.
Recommended video:
Guided course

Rational Exponents
Sum of Squares
The expression x⁴ + y⁴ can be factored using the sum of squares identity, which states that a² + b² can be expressed as (a + bi)(a - bi) in the complex number system. While this is not directly applicable in real numbers, recognizing the structure of the expression can aid in simplification and understanding the underlying algebraic relationships.
Recommended video:

Solving Quadratic Equations by Completing the Square
Related Videos
Related Practice