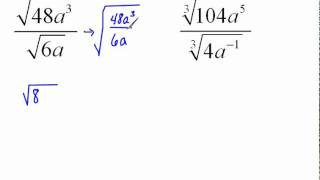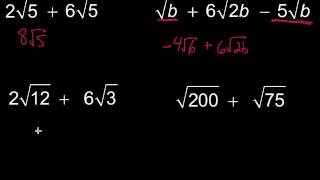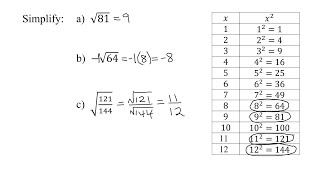Table of contents
- 0. Review of Algebra4h 18m
- 1. Equations & Inequalities3h 18m
- 2. Graphs of Equations1h 43m
- 3. Functions2h 17m
- 4. Polynomial Functions1h 44m
- 5. Rational Functions1h 23m
- 6. Exponential & Logarithmic Functions2h 28m
- 7. Systems of Equations & Matrices4h 5m
- 8. Conic Sections2h 23m
- 9. Sequences, Series, & Induction1h 22m
- 10. Combinatorics & Probability1h 45m
0. Review of Algebra
Radical Expressions
Struggling with College Algebra?
Join thousands of students who trust us to help them ace their exams!Watch the first video
Square Roots
Patrick Ford
Video duration:
5mPlay a video:
Related Videos
Related Practice