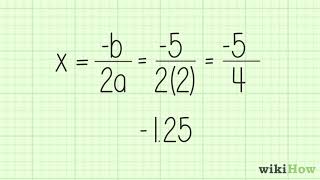Several graphs of the quadratic function ƒ(x) = ax^2 + bx + c are shown below. For the given restrictions on a, b, and c, select the corresponding graph from choices A–F. (Hint: Use the discriminant.) A > 0; b^2 - 4ac > 0

Key Concepts

Quadratic Functions

A quadratic function is a polynomial function of degree two, typically expressed in the form ƒ(x) = ax^2 + bx + c, where a, b, and c are constants. The graph of a quadratic function is a parabola, which opens upwards if a > 0 and downwards if a < 0. Understanding the shape and position of the parabola is essential for analyzing its properties and behavior.

Discriminant

The discriminant of a quadratic equation, given by the formula D = b^2 - 4ac, is a key value that determines the nature of the roots of the equation. If D > 0, the quadratic has two distinct real roots; if D = 0, there is exactly one real root (a repeated root); and if D < 0, the roots are complex and not real. This concept is crucial for predicting the intersection points of the parabola with the x-axis.

Graphical Interpretation

Graphical interpretation involves analyzing the visual representation of mathematical functions. For quadratic functions, this includes understanding how the coefficients a, b, and c affect the vertex, axis of symmetry, and direction of the parabola. By interpreting the graphs in relation to the discriminant and the given conditions, one can select the correct graph that meets the specified criteria.