Use the graph to evaluate each expression. See Example 3(a). (ƒ-g)(1)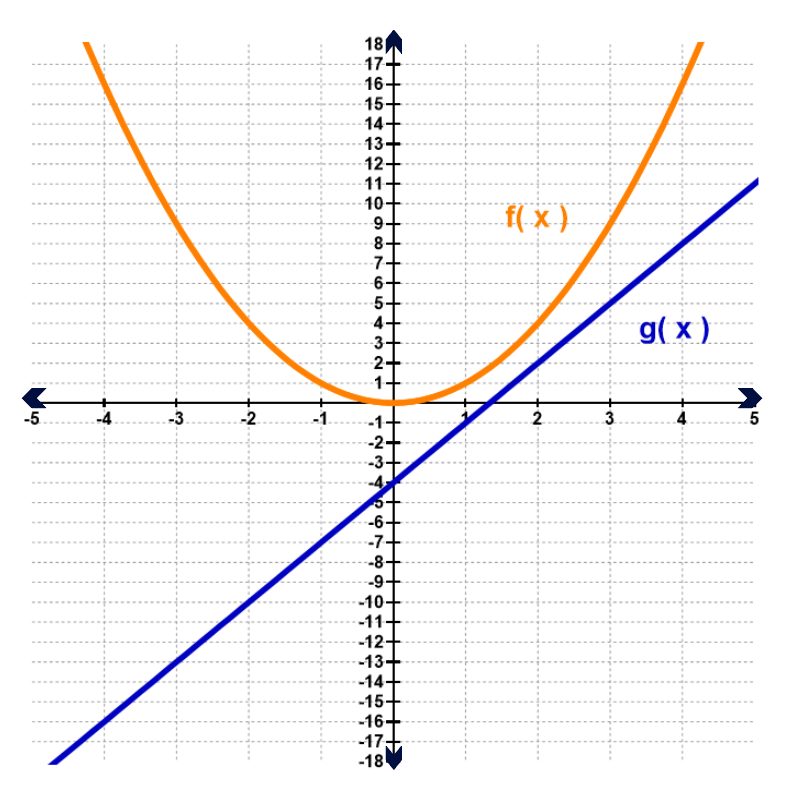

Verified step by step guidance

1. Identify the functions f(x) and g(x) from the graph.
2. Locate the point where x = 1 on the x-axis.
3. Find the value of f(1) by looking at the y-coordinate of the point on the f(x) curve at x = 1.
4. Find the value of g(1) by looking at the y-coordinate of the point on the g(x) line at x = 1.
5. Calculate (f-g)(1) by subtracting g(1) from f(1).

Key Concepts

Function Evaluation

Function evaluation involves substituting a specific input value into a function to determine its output. In this case, evaluating (f-g)(1) requires finding the values of f(1) and g(1) from the graph, and then calculating the difference between these two outputs.

Graph Interpretation

Interpreting graphs is essential for understanding the behavior of functions visually. The graph shows two functions, f(x) and g(x), where f(x) is a quadratic function and g(x) is a linear function. Observing their intersection points and values at specific x-coordinates helps in evaluating expressions involving these functions.

Difference of Functions

The difference of functions, denoted as (f-g)(x), represents a new function created by subtracting the output of g(x) from f(x) for any input x. This concept is crucial for solving the problem, as it requires calculating the values of f and g at x=1 and then finding their difference to evaluate (f-g)(1).