Table of contents
- 0. Review of Algebra4h 16m
- 1. Equations & Inequalities3h 18m
- 2. Graphs of Equations43m
- 3. Functions2h 17m
- 4. Polynomial Functions1h 44m
- 5. Rational Functions1h 23m
- 6. Exponential & Logarithmic Functions2h 28m
- 7. Systems of Equations & Matrices4h 6m
- 8. Conic Sections2h 23m
- 9. Sequences, Series, & Induction1h 19m
- 10. Combinatorics & Probability1h 45m
10. Combinatorics & Probability
Combinatorics
Problem 72
Textbook Question
Textbook QuestionEvaluate the expression. *permutation notation* the number of permutations 8 things taken 3 at a time (sub 8)P(sub 3)
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
2mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
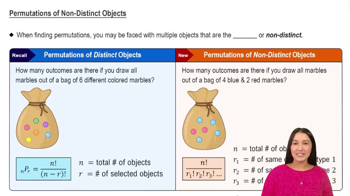
Permutations
Permutations refer to the different ways in which a set of items can be arranged or ordered. In mathematics, the number of permutations of 'n' items taken 'r' at a time is calculated using the formula P(n, r) = n! / (n - r)!, where 'n!' denotes the factorial of 'n'. This concept is crucial for understanding how to count arrangements when the order of selection matters.
Recommended video:

Introduction to Permutations
Factorial
The factorial of a non-negative integer 'n', denoted as 'n!', is the product of all positive integers up to 'n'. For example, 5! = 5 × 4 × 3 × 2 × 1 = 120. Factorials are fundamental in permutations and combinations, as they provide the necessary calculations for determining the total arrangements or selections of items.
Recommended video:

Factorials
Combination vs. Permutation
While both permutations and combinations deal with selecting items from a set, the key difference lies in the importance of order. Permutations consider the arrangement of items as significant, while combinations focus solely on the selection, disregarding order. Understanding this distinction is essential when evaluating expressions involving permutations, as it affects the calculation method used.
Recommended video:

Permutations vs. Combinations

 4:4m
4:4mWatch next
Master Fundamental Counting Principle with a bite sized video explanation from Callie
Start learning