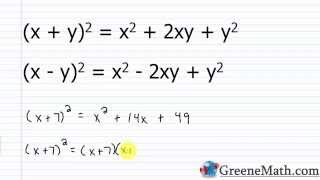Table of contents
- 0. Review of Algebra4h 16m
- 1. Equations & Inequalities3h 18m
- 2. Graphs of Equations43m
- 3. Functions2h 17m
- 4. Polynomial Functions1h 44m
- 5. Rational Functions1h 23m
- 6. Exponential & Logarithmic Functions2h 28m
- 7. Systems of Equations & Matrices4h 6m
- 8. Conic Sections2h 23m
- 9. Sequences, Series, & Induction1h 19m
- 10. Combinatorics & Probability1h 45m
0. Review of Algebra
Multiplying Polynomials
Problem 14
Textbook Question
Textbook QuestionIn Exercises 7–14, simplify each rational expression. Find all numbers that must be excluded from the domain of the simplified rational expression. (x^2−14x+49)/(x^2−49)
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
3mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Rational Expressions
A rational expression is a fraction where both the numerator and the denominator are polynomials. Simplifying these expressions involves factoring both the numerator and the denominator to identify common factors that can be canceled. Understanding how to manipulate these expressions is crucial for solving problems involving them.
Recommended video:
Guided course

Rationalizing Denominators
Factoring Polynomials
Factoring polynomials is the process of breaking down a polynomial into simpler components, or factors, that when multiplied together give the original polynomial. For example, the expression x^2 - 14x + 49 can be factored as (x - 7)(x - 7) or (x - 7)². This skill is essential for simplifying rational expressions and identifying restrictions on the variable.
Recommended video:
Guided course

Introduction to Factoring Polynomials
Domain Restrictions
The domain of a rational expression consists of all the values that the variable can take without making the denominator zero. In the expression (x^2−14x+49)/(x^2−49), the denominator x^2 - 49 factors to (x - 7)(x + 7), indicating that x cannot equal 7 or -7. Identifying these restrictions is vital for understanding the behavior of the expression and ensuring valid solutions.
Recommended video:

Domain Restrictions of Composed Functions
Related Videos
Related Practice