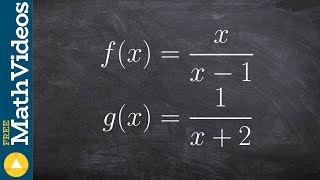Determine whether the given functions are inverses. ƒ= {(2,5), (3,5), (4,5)}; g = {(5,2)}

Key Concepts

Inverse Functions

Inverse functions are pairs of functions that 'undo' each other. For two functions f and g to be inverses, applying g to the output of f should return the original input, and vice versa. This means that for every point (a, b) in f, there should be a corresponding point (b, a) in g. Understanding this relationship is crucial for determining if the given functions are inverses.

Function Representation

Functions can be represented as sets of ordered pairs, where each input is associated with exactly one output. In the given question, f is represented as a set of pairs, indicating that for inputs 2, 3, and 4, the output is consistently 5. Recognizing how functions are represented helps in analyzing their properties and relationships, such as whether they are inverses.

Domain and Range

The domain of a function is the set of all possible input values, while the range is the set of all possible output values. For the functions f and g to be inverses, the range of f must match the domain of g, and the domain of f must match the range of g. In this case, understanding the domain and range of the given functions is essential to verify their inverse relationship.