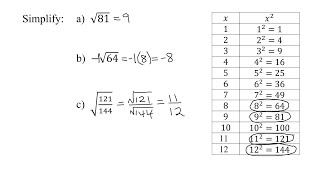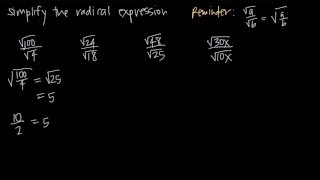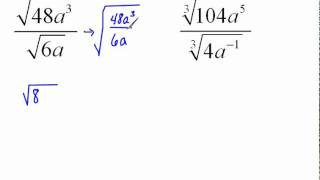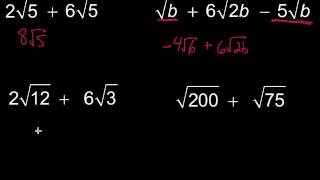Table of contents
- 0. Review of Algebra4h 16m
- 1. Equations & Inequalities3h 18m
- 2. Graphs of Equations43m
- 3. Functions2h 17m
- 4. Polynomial Functions1h 44m
- 5. Rational Functions1h 23m
- 6. Exponential & Logarithmic Functions2h 28m
- 7. Systems of Equations & Matrices4h 6m
- 8. Conic Sections2h 23m
- 9. Sequences, Series, & Induction1h 19m
- 10. Combinatorics & Probability1h 45m
0. Review of Algebra
Radical Expressions
Problem 83b
Textbook Question
Textbook QuestionIn Exercises 79–112, use rational exponents to simplify each expression. If rational exponents appear after simplifying, write the answer in radical notation. Assume that all variables represent positive numbers. _____ ⁵√x¹⁰y¹⁵
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
2mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Rational Exponents
Rational exponents are a way to express roots using fractional powers. For example, the expression x^(1/n) represents the nth root of x. This concept allows for the simplification of expressions involving roots and powers, making calculations more manageable. Understanding how to convert between radical and exponent notation is crucial for solving problems involving rational exponents.
Recommended video:
Guided course

Rational Exponents
Radical Notation
Radical notation is a mathematical notation used to denote roots, such as square roots or cube roots. The radical symbol (√) indicates the root of a number, where the index of the root is specified when it is not a square root. Converting expressions from rational exponents to radical notation is often required in algebra to present answers in a more recognizable form, especially when dealing with roots of variables.
Recommended video:
Guided course

Expanding Radicals
Simplifying Expressions
Simplifying expressions involves reducing them to their simplest form, which often includes combining like terms, reducing fractions, and applying exponent rules. In the context of rational exponents, this means using properties of exponents to rewrite expressions in a more manageable way. Mastery of simplification techniques is essential for effectively solving algebraic problems and ensuring accurate results.
Recommended video:
Guided course

Simplifying Algebraic Expressions
Related Videos
Related Practice