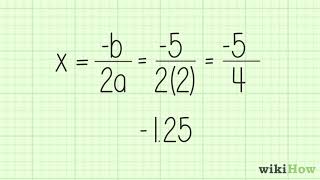Several graphs of the quadratic function ƒ(x) = ax^2 + bx + c are shown below. For the given restrictions on a, b, and c, select the corresponding graph from choices A–F. (Hint: Use the discriminant.) a < 0; b^2 - 4ac = 0

Key Concepts

Quadratic Functions

A quadratic function is a polynomial function of degree two, typically expressed in the form ƒ(x) = ax^2 + bx + c, where a, b, and c are constants. The graph of a quadratic function is a parabola, which opens upwards if a > 0 and downwards if a < 0. Understanding the shape and direction of the parabola is crucial for analyzing its properties and behavior.

Discriminant

The discriminant of a quadratic equation, given by the formula D = b^2 - 4ac, determines the nature of the roots of the equation. If D > 0, there are two distinct real roots; if D = 0, there is exactly one real root (the vertex touches the x-axis); and if D < 0, there are no real roots. In this question, the condition b^2 - 4ac = 0 indicates that the graph will touch the x-axis at one point.

Graphical Interpretation

Graphical interpretation involves understanding how the parameters a, b, and c affect the graph of the quadratic function. For instance, since a < 0, the parabola opens downwards, and the condition b^2 - 4ac = 0 indicates that the vertex of the parabola is at the x-axis, leading to a single point of intersection. This knowledge is essential for selecting the correct graph from the given options.