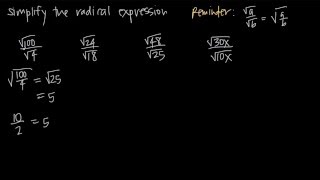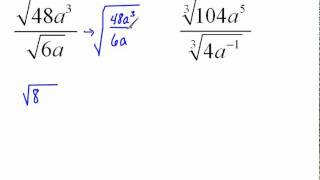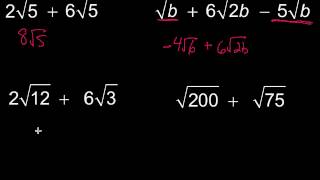In Exercises 59–76, find the indicated root, or state that the expression is not a real number. ___ −⁴√256

Verified step by step guidance

1. Identify the expression: \(-\sqrt[4]{256}\).
2. Recognize that \(\sqrt[4]{256}\) represents the fourth root of 256.
3. Calculate the fourth root of 256 by finding a number that, when raised to the power of 4, equals 256.
4. Determine if the fourth root of 256 is a real number. If it is, then the expression \(-\sqrt[4]{256}\) is also a real number, but negative.
5. If the fourth root of 256 is not a real number, then the expression \(-\sqrt[4]{256}\) is not a real number.

Key Concepts

Radical Expressions

Radical expressions involve roots, such as square roots or fourth roots, which represent the inverse operation of exponentiation. For example, the square root of a number 'x' is a value that, when squared, gives 'x'. Understanding how to manipulate and simplify these expressions is crucial for solving problems involving roots.

Even and Odd Roots

Even roots, like the square root or fourth root, can yield both positive and negative results, but they are typically defined to return only the non-negative root in real numbers. In contrast, odd roots, such as cube roots, can yield negative results. Recognizing the distinction between even and odd roots is essential for determining the nature of the solutions.

Real Numbers

Real numbers include all the rational and irrational numbers that can be found on the number line. When evaluating roots, it is important to determine whether the result is a real number. For instance, the fourth root of a positive number is always a real number, while the fourth root of a negative number is not, as it does not exist within the real number system.