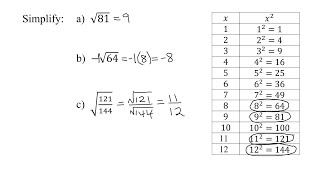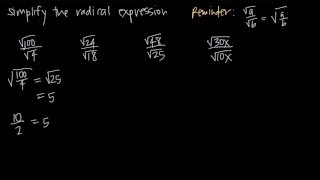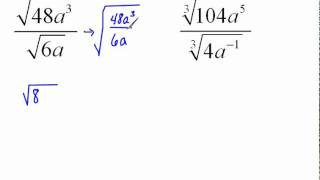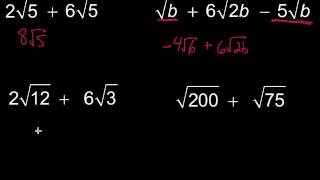Table of contents
- 0. Review of Algebra4h 16m
- 1. Equations & Inequalities3h 18m
- 2. Graphs of Equations43m
- 3. Functions2h 17m
- 4. Polynomial Functions1h 44m
- 5. Rational Functions1h 23m
- 6. Exponential & Logarithmic Functions2h 28m
- 7. Systems of Equations & Matrices4h 6m
- 8. Conic Sections2h 23m
- 9. Sequences, Series, & Induction1h 19m
- 10. Combinatorics & Probability1h 45m
0. Review of Algebra
Radical Expressions
Problem 5b
Textbook Question
Textbook QuestionIn Exercises 1–20, use radical notation to rewrite each expression. Simplify, if possible. -16^¼
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
3mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Radical Notation
Radical notation is a mathematical notation used to represent roots of numbers. The symbol '√' denotes the square root, while 'n√' represents the nth root of a number. For example, the expression 'x^(1/n)' can be rewritten as 'n√x', indicating the nth root of x. Understanding this notation is essential for rewriting expressions involving roots.
Recommended video:
Guided course

Expanding Radicals
Exponents and Fractional Powers
Exponents are a way to express repeated multiplication of a number by itself. A fractional exponent, such as '1/4', indicates a root; specifically, 'x^(1/n)' means the nth root of x. In the case of '-16^(1/4)', it signifies the fourth root of -16, which is crucial for simplifying the expression correctly.
Recommended video:

Powers of i
Simplifying Radical Expressions
Simplifying radical expressions involves reducing them to their simplest form, which often includes factoring out perfect squares or cubes. For instance, when simplifying '√(a*b)', one can separate it into '√a * √b'. In the context of '-16^(1/4)', recognizing that -16 can be expressed as '(-1) * (16)' helps in simplifying the expression further.
Recommended video:
Guided course

Radical Expressions with Fractions
Related Videos
Related Practice