Table of contents
- 0. Review of Algebra4h 16m
- 1. Equations & Inequalities3h 18m
- 2. Graphs of Equations43m
- 3. Functions2h 17m
- 4. Polynomial Functions1h 44m
- 5. Rational Functions1h 23m
- 6. Exponential & Logarithmic Functions2h 28m
- 7. Systems of Equations & Matrices4h 6m
- 8. Conic Sections2h 23m
- 9. Sequences, Series, & Induction1h 19m
- 10. Combinatorics & Probability1h 45m
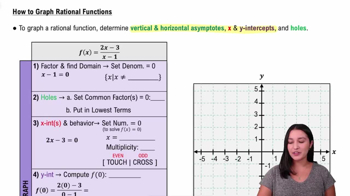
5. Rational Functions
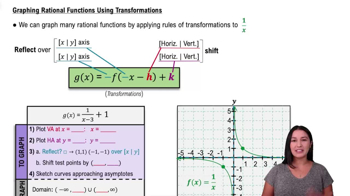
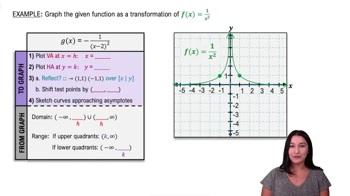
Graphing Rational Functions
Problem 23
Textbook Question
In Exercises 21–36, find the vertical asymptotes, if any, and the values of x corresponding to holes, if any, of the graph of each rational function. g(x)=(x+3)/x(x+4)
 Verified step by step guidance
Verified step by step guidance1
Identify the rational function: \( g(x) = \frac{x+3}{x(x+4)} \).
Determine the values of \( x \) that make the denominator zero, as these are potential vertical asymptotes or holes. Set \( x(x+4) = 0 \) and solve for \( x \).
Solve the equation \( x(x+4) = 0 \) to find \( x = 0 \) and \( x = -4 \).
Check if these values also make the numerator zero. If a value makes both the numerator and denominator zero, it corresponds to a hole. Otherwise, it is a vertical asymptote.
Since \( x = 0 \) and \( x = -4 \) do not make the numerator zero, these values correspond to vertical asymptotes.
Recommended similar problem, with video answer:
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
1mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Rational Functions
A rational function is a function that can be expressed as the ratio of two polynomials. In the given function g(x) = (x + 3) / (x(x + 4)), the numerator is a polynomial of degree 1, and the denominator is a polynomial of degree 2. Understanding the structure of rational functions is essential for analyzing their behavior, including identifying asymptotes and holes.
Recommended video:

Intro to Rational Functions
Vertical Asymptotes
Vertical asymptotes occur in a rational function when the denominator approaches zero while the numerator does not simultaneously approach zero. For g(x), we find vertical asymptotes by setting the denominator x(x + 4) equal to zero, leading to the values of x that cause the function to be undefined. These values indicate where the graph will approach infinity.
Recommended video:

Determining Vertical Asymptotes
Holes in the Graph
Holes in the graph of a rational function occur at values of x that make both the numerator and denominator equal to zero, indicating a removable discontinuity. In g(x), if the numerator (x + 3) shares a common factor with the denominator, it will create a hole. Identifying these values is crucial for accurately sketching the graph and understanding its behavior.
Recommended video:
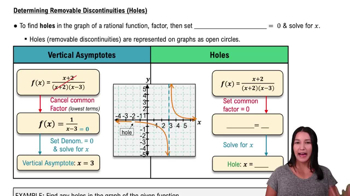
Determining Removable Discontinuities (Holes)

 5:31m
5:31mWatch next
Master Graphing Rational Functions Using Transformations with a bite sized video explanation from Callie
Start learningRelated Videos
Related Practice