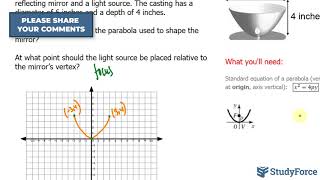
In Exercises 63–68, find the solution set for each system by graphing both of the system's equations in the same rectangular coordinate system and finding points of intersection. Check all solutions in both equations. x = y^2 - 3 x = y^2 - 3y

Key Concepts

Graphing Equations

Graphing equations involves plotting points on a coordinate plane to visualize the relationship between variables. For the given equations, x = y^2 - 3 and x = y^2 - 3y, students must understand how to convert these equations into a graphable form, identifying key features such as intercepts and the shape of the curves.

Points of Intersection

Points of intersection occur where two graphs meet, representing solutions to the system of equations. To find these points, one must solve the equations simultaneously, either algebraically or graphically, and identify the coordinates where the two curves intersect, which indicates the values of x and y that satisfy both equations.

Checking Solutions

Checking solutions involves substituting the found intersection points back into the original equations to verify their validity. This step ensures that the identified points are indeed solutions to both equations, confirming that they satisfy the conditions of the system and are not extraneous solutions.