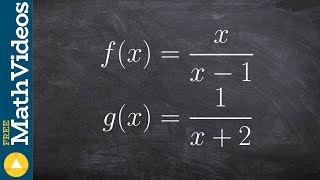Use the graphs of f and g to solve Exercises 83–90.
Find (f+g)(−3).

Key Concepts

Function Addition

Function addition involves combining two functions, f(x) and g(x), to create a new function (f + g)(x). This new function is defined as (f + g)(x) = f(x) + g(x) for all x in the domain of both functions. To find (f + g)(-3), you need to evaluate f(-3) and g(-3) from their respective graphs and then sum these values.

Evaluating Functions from Graphs

To evaluate a function at a specific point using its graph, locate the x-value on the horizontal axis and find the corresponding y-value on the graph. For instance, to find f(-3) and g(-3), you would look for the point where x = -3 on the graphs of f and g, respectively, and read off the y-values. This process is essential for determining the values needed for function addition.

Graph Interpretation

Interpreting graphs involves understanding the visual representation of functions, including their shapes, intersections, and behaviors at specific points. In this case, recognizing how the graphs of f(x) and g(x) interact at x = -3 is crucial for accurately determining the values of f(-3) and g(-3). This skill is fundamental in analyzing and solving problems related to function operations.