Table of contents
- 0. Review of Algebra4h 16m
- 1. Equations & Inequalities3h 18m
- 2. Graphs of Equations43m
- 3. Functions2h 17m
- 4. Polynomial Functions1h 44m
- 5. Rational Functions1h 23m
- 6. Exponential & Logarithmic Functions2h 28m
- 7. Systems of Equations & Matrices4h 6m
- 8. Conic Sections2h 23m
- 9. Sequences, Series, & Induction1h 19m
- 10. Combinatorics & Probability1h 45m
7. Systems of Equations & Matrices
Introduction to Matrices
Problem 23b
Textbook Question
In Exercises 21–38, solve each system of equations using matrices. Use Gaussian elimination with back-substitution or Gauss-Jordan elimination. 
 Verified step by step guidance
Verified step by step guidance1
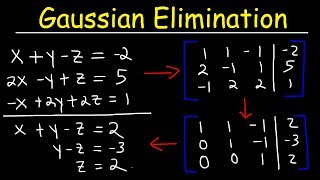
Write the system of equations as an augmented matrix: \( \begin{bmatrix} 1 & 3 & 0 & | & 0 \\ 1 & 1 & 1 & | & 1 \\ 3 & -1 & -1 & | & 11 \end{bmatrix} \).
Use Gaussian elimination to create zeros below the first pivot (1,1) by replacing row 2 with (row 2 - row 1) and row 3 with (row 3 - 3*row 1).
Simplify the matrix to get: \( \begin{bmatrix} 1 & 3 & 0 & | & 0 \\ 0 & -2 & 1 & | & 1 \\ 0 & -10 & -1 & | & 11 \end{bmatrix} \).
Use row operations to create a zero below the second pivot (2,2) by replacing row 3 with (row 3 - 5*row 2).
Simplify the matrix to get: \( \begin{bmatrix} 1 & 3 & 0 & | & 0 \\ 0 & -2 & 1 & | & 1 \\ 0 & 0 & -6 & | & 16 \end{bmatrix} \) and use back-substitution to solve for \( z \), \( y \), and \( x \).
Recommended similar problem, with video answer:
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
13mPlay a video:
Was this helpful?

 4:35m
4:35mWatch next
Master Introduction to Matrices with a bite sized video explanation from Patrick Ford
Start learningRelated Videos
Related Practice