Table of contents
- 0. Review of Algebra4h 16m
- 1. Equations & Inequalities3h 18m
- 2. Graphs of Equations43m
- 3. Functions2h 17m
- 4. Polynomial Functions1h 44m
- 5. Rational Functions1h 23m
- 6. Exponential & Logarithmic Functions2h 28m
- 7. Systems of Equations & Matrices4h 6m
- 8. Conic Sections2h 23m
- 9. Sequences, Series, & Induction1h 19m
- 10. Combinatorics & Probability1h 45m
0. Review of Algebra
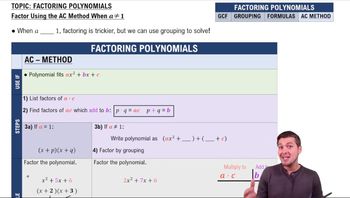
Factoring Polynomials
Problem 83
Textbook Question
Textbook QuestionIn Exercises 65–92, factor completely, or state that the polynomial is prime. 20y^4−45y^2
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
3mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Factoring Polynomials
Factoring polynomials involves breaking down a polynomial expression into simpler components, or factors, that when multiplied together yield the original polynomial. This process often includes identifying common factors, applying special factoring techniques like difference of squares, or using methods such as grouping. Understanding how to factor is essential for simplifying expressions and solving polynomial equations.
Recommended video:
Guided course

Introduction to Factoring Polynomials
Greatest Common Factor (GCF)
The Greatest Common Factor (GCF) is the largest factor that divides two or more numbers or terms without leaving a remainder. In polynomial expressions, finding the GCF allows for the simplification of the polynomial by factoring it out, making it easier to work with. For the polynomial in the question, identifying the GCF is the first step in the factoring process.
Recommended video:

Graphs of Common Functions
Prime Polynomials
A prime polynomial is a polynomial that cannot be factored into simpler polynomials with real coefficients. This means that the polynomial does not have any factors other than itself and 1. Recognizing whether a polynomial is prime is crucial in algebra, as it determines the methods available for solving equations or simplifying expressions.
Recommended video:
Guided course

Introduction to Factoring Polynomials

 7:30m
7:30mWatch next
Master Introduction to Factoring Polynomials with a bite sized video explanation from Patrick Ford
Start learningRelated Videos
Related Practice