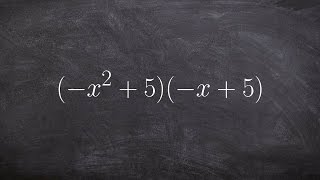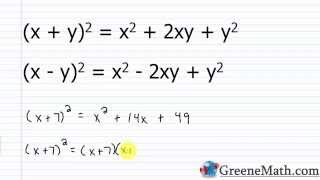Table of contents
- 0. Review of Algebra4h 16m
- 1. Equations & Inequalities3h 18m
- 2. Graphs of Equations43m
- 3. Functions2h 17m
- 4. Polynomial Functions1h 44m
- 5. Rational Functions1h 23m
- 6. Exponential & Logarithmic Functions2h 28m
- 7. Systems of Equations & Matrices4h 6m
- 8. Conic Sections2h 23m
- 9. Sequences, Series, & Induction1h 19m
- 10. Combinatorics & Probability1h 45m
0. Review of Algebra
Multiplying Polynomials
Problem 74a
Textbook Question
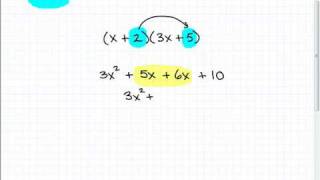
Textbook QuestionIn Exercises 69–82, multiply using the rule for the product of the sum and difference of two terms. (8x + 7y)(8x − 7y)
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
5mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Product of Sum and Difference
The product of the sum and difference of two terms follows the formula (a + b)(a - b) = a² - b². This identity simplifies the multiplication of expressions where one is the sum and the other is the difference of the same two terms, allowing for a quick calculation without expanding the entire expression.
Recommended video:
Guided course

Special Products - Cube Formulas
Algebraic Expressions
Algebraic expressions are combinations of numbers, variables, and operations. In the given expression (8x + 7y)(8x - 7y), the terms 8x and 7y are variables that can represent any real numbers, and understanding how to manipulate these expressions is fundamental in algebra.
Recommended video:
Guided course

Introduction to Algebraic Expressions
Factoring and Expanding
Factoring involves rewriting an expression as a product of its factors, while expanding is the process of multiplying out the factors to form a single expression. Mastery of both concepts is essential for solving algebraic problems, as they allow for simplification and manipulation of expressions effectively.
Recommended video:
Guided course

Factor by Grouping
Related Videos
Related Practice