Table of contents
- 0. Review of Algebra4h 16m
- 1. Equations & Inequalities3h 18m
- 2. Graphs of Equations43m
- 3. Functions2h 17m
- 4. Polynomial Functions1h 44m
- 5. Rational Functions1h 23m
- 6. Exponential & Logarithmic Functions2h 28m
- 7. Systems of Equations & Matrices4h 6m
- 8. Conic Sections2h 23m
- 9. Sequences, Series, & Induction1h 19m
- 10. Combinatorics & Probability1h 45m
2. Graphs of Equations
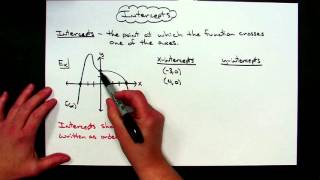
Graphs and Coordinates
Problem 55
Textbook Question
Graph each function. Give the domain and range. See Example 3. ƒ(x)=[[2x]]
 Verified step by step guidance
Verified step by step guidance1
Step 1: Understand the function. The function given is ƒ(x)=[[2x]], which is a greatest integer function. The greatest integer function, also known as the floor function, rounds down a real number to the largest integer less than or equal to the number. For example, the greatest integer of 2.3 is 2, and the greatest integer of -2.3 is -3.
Step 2: Identify the domain. The domain of a function is the set of all possible input values (x-values) which will produce a valid output. For the greatest integer function, the domain is all real numbers, because you can take the greatest integer of any real number. So, the domain of ƒ(x)=[[2x]] is all real numbers.
Step 3: Identify the range. The range of a function is the set of all possible output values (y-values). For the greatest integer function, the range is all integers, because the greatest integer of any real number is an integer. So, the range of ƒ(x)=[[2x]] is all integers.
Step 4: Graph the function. To graph the function, you can start by making a table of values. Choose some x-values, calculate the corresponding y-values using the function, and then plot these points on the graph. Because this is a greatest integer function, the graph will be a series of steps. Each step goes from one integer to the next, and the height of each step is the y-value of the function at that point.
Step 5: Remember that for the greatest integer function, the graph is a closed circle on the left (or at the bottom) of each step and an open circle on the right (or at the top) of each step. This is because the greatest integer function rounds down to the nearest integer. So, for example, the greatest integer of 2.9999 is still 2, not 3.
Recommended similar problem, with video answer:
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
14mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Graphing Functions
Graphing functions involves plotting points on a coordinate plane to visually represent the relationship between the input (x-values) and output (y-values) of a function. Understanding how to interpret the shape and behavior of different types of functions, such as linear, quadratic, or piecewise, is essential for accurately graphing them.
Recommended video:

Graphs of Logarithmic Functions
Domain and Range
The domain of a function refers to the set of all possible input values (x-values) that the function can accept, while the range is the set of all possible output values (y-values) that the function can produce. Identifying the domain and range is crucial for understanding the limitations and behavior of the function, especially in cases where certain values may lead to undefined outputs.
Recommended video:

Domain & Range of Transformed Functions
Greatest Integer Function
The greatest integer function, denoted as [[x]], returns the largest integer less than or equal to x. This function is also known as the floor function. Understanding how this function behaves is important for graphing it accurately, as it creates a step-like graph where each step corresponds to an integer value, affecting both the domain and range.
Recommended video:

Intro to Rational Functions

 5:10m
5:10mWatch next
Master Graphs & the Rectangular Coordinate System with a bite sized video explanation from Patrick Ford
Start learningRelated Videos
Related Practice