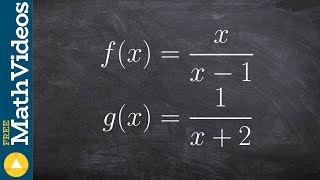Table of contents
- 0. Review of Algebra4h 16m
- 1. Equations & Inequalities3h 18m
- 2. Graphs of Equations43m
- 3. Functions2h 17m
- 4. Polynomial Functions1h 44m
- 5. Rational Functions1h 23m
- 6. Exponential & Logarithmic Functions2h 28m
- 7. Systems of Equations & Matrices4h 6m
- 8. Conic Sections2h 23m
- 9. Sequences, Series, & Induction1h 19m
- 10. Combinatorics & Probability1h 45m
3. Functions
Function Composition
Problem 124b
Textbook Question
Textbook QuestionExercises 123–125 will help you prepare for the material covered in the next section. Solve for y : x = 5/y + 4
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
5mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Solving Equations
Solving equations involves finding the value of a variable that makes the equation true. In this case, we need to isolate 'y' in the equation x = 5/y + 4. This process typically includes rearranging the equation, using algebraic operations such as addition, subtraction, multiplication, and division to isolate the variable of interest.
Recommended video:

Solving Logarithmic Equations
Reciprocal Relationships
The concept of reciprocals is crucial when dealing with fractions and variables. The reciprocal of a number is 1 divided by that number. In the equation x = 5/y + 4, understanding how to manipulate the term 5/y is essential, as it can be rewritten in terms of y by multiplying both sides by y to eliminate the fraction.
Recommended video:
Guided course

Parallel & Perpendicular Lines
Linear Equations
Linear equations are equations of the first degree, meaning they involve variables raised only to the first power. The equation x = 5/y + 4 can be transformed into a linear form by eliminating the fraction and rearranging terms. Recognizing the structure of linear equations helps in applying methods for solving them, such as substitution or elimination.
Recommended video:

Categorizing Linear Equations

 4:56m
4:56mWatch next
Master Function Composition with a bite sized video explanation from Nick Kaneko
Start learningRelated Videos
Related Practice