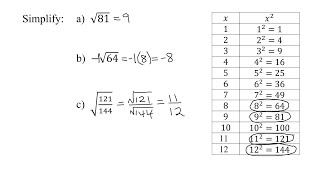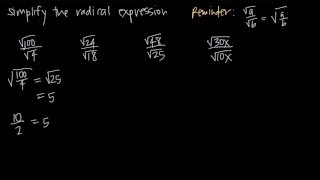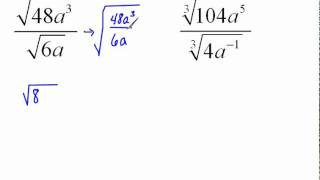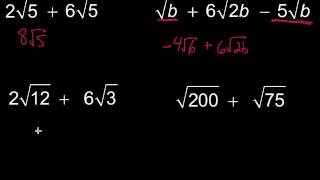In Exercises 1–20, use the product rule to multiply. ___ ___ √x+6 ⋅ √x-6

Key Concepts

Product Rule

The product rule is a fundamental principle in algebra that states when multiplying two expressions, you can apply the distributive property. This involves multiplying each term in the first expression by each term in the second expression. In this case, it helps to simplify the multiplication of square roots by treating them as separate entities before combining them.

Square Roots

Square roots are a mathematical operation that finds a number which, when multiplied by itself, gives the original number. In this problem, the expressions involve square roots of 'x + 6' and 'x - 6'. Understanding how to manipulate square roots, including their properties and how they interact with addition and subtraction, is crucial for simplifying the expression correctly.

Difference of Squares

The difference of squares is a specific algebraic identity that states a² - b² = (a + b)(a - b). This concept is particularly relevant here, as the multiplication of √(x + 6) and √(x - 6) can be recognized as a difference of squares. Recognizing this allows for a more straightforward simplification of the expression, leading to a clearer solution.